Przeszukaj forum
Pokazywanie wyników dla tagów 'processing'.
Znaleziono 7 wyników
-
Część Czwarta W poprzedniej części omówione zostało wypełnianie obiektów trójwymiarowych teksturą oraz przedstawione wybrane funkcje światła. W ostatniej już, czwartej części, program uzupełnimy o funkcje umożliwiające obejrzenie całego modelu ze wszystkich stron przy wykorzystaniu komputerowej myszki. Obrotu widoku sceny można dokonać na 2 podstawowe sposoby: 1. bezpośrednie przekształcenia obiektów w przestrzeni trójwymiarowej; 2. zmianę położenia obserwatora (kamery) patrzącego na nieruchome obiekty. Do programu zaimplementowane zostały obydwa sposoby. Przy czym, transformacja obiektów została wprowadzona w wersji: (1) - „dla wymagających”. Natomiast, przesunięcia kamery w wersji (2) - „dla leniwych”, przy wykorzystaniu biblioteki zewnętrznej. Bez względu na wybraną metodę końcowy efekt będzie podobny, ale nie identyczny. PMatrix3D, PVector W pierwszej kolejności zajmiemy się „wersją dla wymagających”. Naszym celem jest wyposażenie programu w możliwość jednoczesnego obracania wszystkich elementów znajdujących się na scenie wokół dowolnej osi i o dowolny kąt za pośrednictwem myszki. Innymi słowy, chcemy dokonywać transformacji położenia wszystkich obiektów razem, względem nieruchomego obserwatora zależnie od położenia kursora myszki. Rozwiązania intuicyjne tego zadania nie zawsze prowadzą do oczekiwanych wyników. Najczęściej, o ile nie zostaną zastosowane restrykcyjne reguły transformacji, układ Ziemia-Słońce będzie zmieniał swoje położenie z trudnymi do okiełznania aberracjami… Na szczęście teorię przekształceń w przestrzeni 3D można znaleźć w każdym akademickim podręczniku geometrii lub ją sobie wymyślić i tym samym nie ma potrzeby jej tutaj przytaczać. Bardziej zainteresowanych tematem z przyjemnością odsyłam do artykułu: 3D Rotations in Processing (Vectors, Matrices, Quaternions) , można w nim znaleźć dość przejrzyście wyjaśnioną teorię stosowaną do przesunięć w przestrzeni 3D, wraz z propozycjami jej implementacji. Tutaj zajmiemy się wyłącznie zastosowaniami praktycznymi. Krótki, prosty i co najważniejsze efektywny algorytm obrotu przestrzeni 3D o zadany wektor jest następujący: Krok 1 Zainicjowanie macierzy współrzędnych jednorodnych (MATRIX): Inicjalizacja macierzy będzie polegała na przypisaniu macierzy współrzędnej czterowymiarowej macierzy jednostkowej: PMatrix3D MATRIX=new PMatrix3D // Inicjalizacja obiektu MATRIX klasy PMatrix3D (macierz przestrzeni 3D w ujęciu jednorodnym) (1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1); Wykorzystana została do tego nieudokumentowana klasa PMatrix3D (próżno, szukać więcej informacji o niej na stronie processing.org) lakoniczny opis znajdziemy pod adresem: Class PMatrix3D Funkcja new w Processing służy do tworzenia nowego obiektu zadanej klasy. Utworzoną macierz można rozumieć jako macierz przekształceń przestrzeni. Przekształcenia te wkrótce nastąpią. Krok 2 Zainicjowanie wektora obrotu (rotationVector) Wektor będzie przechowywał informacje o przesunięciach wskaźnika myszki w płaszczyźnie ekranu X, Y. Świadomie pomijamy tu wartość Z. Nie będzie ona na razie potrzebna i przypisujemy jej na stałe wartość 0. PVector rotationVector=new PVector (0,0,0); // Inicjalizacja obiektu rotationVector klasy PVector (wektor obrotu) PVector jest klasą opisującą dwu lub trójwymiarowy wektor geometryczny znany ze szkoły podstawowej posiadający moduł i kierunek. Podobnie jak obiekt klasy PMatrix3D należy go utworzyć przy wykorzystaniu funkcji new. Krok 3 Aktualizacja wektora obrotu(rotationVector) Wartość X wektora zastąpiona zostaje zmianą położenia myszki wzdłuż osi X Wartość Y wektora zastąpiona zostaje zmianą położenia myszki wzdłuż osi Y Do aktualizacji wektora rotationVector posłuży nam przerwanie obsługujące przeciągnięcie myszki wywoływane funkcją mouseDragged(). Processing przechowuje dwie pomocne zmienne systemowe mouseX oraz pmouseX reprezentujące odpowiednio bieżące oraz poprzednie położenie wskaźnika myszki. Podobnie dzieje się w przypadku współrzędnej Y gdzie zmienne przyjmują oznaczenie mouseY i pmouseY. W naszym przypadku funkcja ma następującą postać: void mouseDragged() { // Funkcja obsługująca przerwanie wywołane przeciągnięciem myszki z wciśniętym przyciskiem rotationVector.x=(pmouseY-mouseY); // Przypisanie współrzędnej X wektora obrotu wartości przesunięcia myszki wzdłuż osi X rotationVector.y=(mouseX-pmouseX); // Przypisanie współrzędnej X wektora obrotu wartości przesunięcia myszki wzdłuż osi Y } Krok 4 Transpozycja macierzy (MATRIX) Zamiana wierszy na kolumny i kolumn na wiersze metodą transpose() klasy PMatrix3D: MATRIX.transpose(); // Transpozycja macierzy 3D Krok 5 Przemnożenie macierzy (MATRIX) przez wektor obrotu (rotationVector) W wyniku mnożenia otrzymujemy nowy, zmodyfikowany wektor obrotu (rotationVector). MATRIX.mult(rotationVector,rotationVector); // Aktualizacja wartości wektora obrotu poprzez przemnożenie go przez macierz przestrzeni Krok 6 Ponowna transpozycja macierzy (MATRIX) Przywrócenie macierzy do pierwotnej formy. Ponieważ pierwsza transpozycja służyła nam wyłącznie do wykonania mnożenia macierzy przez wektor jeszcze raz zamieniamy jej kolumny z wierszami i wiersze z kolumnami. Krok 7 Obrót macierzy współrzędnych (MATRIX) o zadany kąt wokół wektora powstałego ze współrzędnych X,Y,Z wektora obrotu (rotationVector) Kąt ustalony jest arbitralnie (np. 2PI/360*5). Determinuje skalę obrotu w reakcji na ruch myszką. W wyniku obrotu zawartość MATRIX aktualizuje się o nowe wartości. MATRIX.rotate(TWO_PI/360*6,rotationVector.x,rotationVector.y,rotationVector.z); // Obrót macierzy o kąt 6 stopni wokół zmodyfikowanego wektora x,y,z Kąt obrotu będzie decydował o „czułości” myszki. Im większe będzie jej przesunięcie, tym większa będzie jednorazowa skala obrotu obiektu. Krok 8 Transformacja bieżącego układu współrzędnych macierzą MATRIX Wykonujemy mnożenie bieżącego układu współrzędnych (bieżącej macierzy) przez macierz transformacji (MATRIX). Jak ostrzega Processing funkcja jest bardzo powolna, ponieważ próbuje obliczyć odwrotność transformacji. Dla naszego programu jest jednak wystarczająco szybka, teoretycznie można ją też sobie samemu napisać, ale oczywiście zajmie to kolejne linijki kodu. applyMatrix(MATRIX); // Zastąpienie bieżącej przestrzeni 3D przestrzenią przekształconą 3D Krok 9 Reset wektora obrotu Przywrócenie wektora do pierwotnej postaci 0,0,0: rotationVector.set(0,0,0); // Reset wektora obrotu Na tym kończy się algorytm. Oczywiście istnieje wiele różnych implementacji teorii obrotów w praktyce programowania. Ta akurat jest własną metodą autorską. Proponowane, dostępne w sieci, implementacje są zawsze(nie do końca wiadomo dlaczego) dużo bardziej skomplikowane i często nieczytelne. Po zastosowaniu obrotów program przyjmuje następującą formę: PMatrix3D MATRIX=new PMatrix3D // Inicjalizacja obiektu MATRIX klasy PMatrix3D (macierz przestrzeni 3D w ujęciu jednorodnym) (1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1); PVector rotationVector= new PVector (0,0,0); // Inicjalizacja obiektu rotationVector klasy PVector (wektor obrotu) int EARTH_RADIUS=150; // Promień Ziemi int SUN_RADIUS=10; // Promień Słońca int SUN_ORBIT=300; // Promień orbity Słońca; int CELESTIAL_SPHERE_RADIUS=4000; // Promień Sfery Niebieskiej float xSol=0; // Chwilowa współrzędna x środka Śłońca float ySol=0; // Chwilowa współrzędna y środka Śłońca float zSol=0; // Chwilowa współrzędna z środka Śłońca float tSol=0; // Chwilowy azymut Słońca liczony od południka 0 w radianach PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemi PImage EARTH_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Ziemi PShape SUN; // Deklaracja kształtu przechowującego informacje o kształcie Słońca PImage SUN_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Słońca PShape CELESTIAL_SPHERE; // Deklaracja kształtu przechowującego informacje o kształcie Sfery Niebieskiej PImage CELESTIAL_SPHERE_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Sfery Niebieskiej void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło smooth(4); // Ustawienie poziomu anty-aliasingu sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); EARTH_TEXTURE=loadImage("1_earth_8k.jpg"); //EARTH_TEXTURE=loadImage("http://shadedrelief.com/natural3/ne3_data/8192/textures/1_earth_8k.jpg"); SUN=createShape(SPHERE, SUN_RADIUS); SUN_TEXTURE=loadImage("320px-Map_of_the_full_sun.jpg"); //SUN_TEXTURE=loadImage("https://upload.wikimedia.org/wikipedia/commons/thumb/9/99/Map_of_the_full_sun.jpg/320px-Map_of_the_full_sun.jpg"); CELESTIAL_SPHERE=createShape(SPHERE, CELESTIAL_SPHERE_RADIUS); CELESTIAL_SPHERE_TEXTURE=loadImage("eso0932a.jpg"); //CELESTIAL_SPHERE_TEXTURE=loadImage("https://cdn.eso.org/images/large/eso0932a.jpg"); EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setTexture(EARTH_TEXTURE); // Przypisanie tekstury kształtowi Ziemi SUN.setStroke(false); // Brak wyświetlania obrysu SUN.setTexture(SUN_TEXTURE); // Przypisanie tekstury kształtowi Słońca CELESTIAL_SPHERE.setStroke(false); // Brak wyświetlania obrysu CELESTIAL_SPHERE.setTexture(CELESTIAL_SPHERE_TEXTURE); // Przypisanie tekstury kształtowi Sfery Niebieskiej } void draw() { background(22); translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu MATRIX.transpose(); // Transpozycja macierzy przestrzeni 3D MATRIX.mult(rotationVector,rotationVector); // Aktualizacja wartości wektora obrotu poprzez przemnożenie go przez macierz przestrzeni MATRIX.transpose(); // Ponowna transpozycja macierzy MATRIX.rotate(TWO_PI/360*6,rotationVector.x,rotationVector.y,rotationVector.z); // Obrót macierzy o kąt 6 stopni wokół zmodyfikowanego wektora x,y,z applyMatrix(MATRIX); // Zastąpienie bieżącej przestrzeni 3D przestrzenią przekształconą 3D rotationVector.set(0,0,0); // Reset wektora obrotu rotateX(TWO_PI/4); // Obrót środka układu współrzędnych o 90 stopni wokół osi X rotateZ(TWO_PI/4); // Obrót środka układu współrzędnych o 90 stopni wokół osi Z pushMatrix(); rotateY(TWO_PI/12); rotateZ(TWO_PI/6); shape(CELESTIAL_SPHERE); popMatrix(); directionalLight(255, 255, 210, -xSol, -ySol, -zSol); // Oświetlenie Ziemi światłem jasnożółtym padającym z kierunku Słońca pushMatrix(); // Wepchnięcie macierzy współrzędnych rotateX(-TWO_PI/4); // Obrót środka układu współrzędnych o -90 stopni wokół osi X rotateY(PI); // Obrót środka układu współrzędnych o 180 stopni wokół osi Y ambientLight(28, 28, 28); // Przyciemnienie Ziemi shape(EARTH); // Wyświetlenie obrazu Ziemi lights(); // Reset ustawień funkcji światła popMatrix(); // Wypchnięcie macierzy współrzędnych xSol=SUN_ORBIT*cos(tSol); // Określenie pozycji X środka Słońca ySol=SUN_ORBIT*sin(tSol); // Określenie pozycji Y środka Słońca tSol+=TWO_PI/360; // Ustalenie azymutu Słońca if (tSol>TWO_PI) tSol=0; // Reset azymutu po zakreśleniu przez słońce pełnej orbity pushMatrix(); // Wepchnięcie macierzy współrzędnych translate(xSol,ySol,zSol); // Przesunięcie środka układu współrzędnych do miejsca położenia Słońca ambientLight(255, 255, 210); // Rozświetlenie Słońca shape(SUN); // Wyświetlenie obrazu Słońca lights(); // Reset ustawień funkcji światła popMatrix(); // Wypchnięcie macierzy współrzędnych } void mouseDragged() { // Funkcja obsługująca przerwanie wywołane przeciągnięciem myszki z wciśniętym klawiszem rotationVector.x=(pmouseY-mouseY); // Przypisanie współrzędnej x wektora obrotu wartości przesunięcia myszki wzdłuż osi X rotationVector.y=(pmouseX-mouseX); // Przypisanie współrzędnej y wektora obrotu wartości przesunięcia myszki wzdłuż osi Y } void mouseClicked(MouseEvent event) { // Funkcja obsługująca przerwanie wywołane kliknięciem myszki if (event.getCount() >= 2) MATRIX.reset(); // Przywrócenie Ziemi pierwotnego położenia po dwukrotnym kliknięciu myszką } Na końcu skryptu umieszczona została dodatkowo funkcja obsługująca kliknięcie myszką. Za jej pomocą można, po drobnej modyfikacji, dokonać resetu macierzy układu w wyniku dwukrotnego kliknięcia myszką. Efekt przedstawia się następująco: Do pełni efektu pozornie brakuje jeszcze obsługi ruchu układu względem osi Z np. przy wykorzystaniu ruchu kółka myszki. Tutaj jednak stajemy przed dylematem: czy obrót kółka ma dokonywać obrotu układu względem osi o kąt odpowiadający obrotowi kółka, czy też ma powodować ruch obserwatora wzdłuż osi Z. W zasadzie trzymając się założenia, że operujemy układem, a nie obserwatorem, dylemat brzmi czy ruch kółka powinien obracać układ, czy też powodować jego „puchnięcie” lub „kurczenie”. Kwestia ta pozostawiona została Czytelnikowi do samodzielnego rozstrzygnięcia i ew. implementacji. Można do tego wykorzystać funkcję obsługi przerwania: mouseWheel(). W naszym programie kółko myszki zostanie wykorzystane do innych celów, a ruch obiektu względem osi Z nie zostanie oprogramowany jako, akurat w tym przypadku, zupełnie niepotrzebny. peasycam ver302 Jak zostało podkreślone na wstępie efekt ruchu (obrotu) układu w zależności od ruchu myszki można wywołać poruszając samym układem lub poruszając obserwatorem. W naszym programie zastosujemy na raz obydwie metody, czyli możliwe będzie zarówno poruszanie obiektami jak i przesuwanie obserwującej je kamerą. Zaczynamy od drobnej modyfikacji funkcji przeciągania myszki ograniczając obroty obiektów wyłącznie do prawego klawisza. W ten sposób pozostawiamy lewy klawisz i kółko do swobodnego wykorzystania. Możemy ich użyć na przykład do obrotów kamerą i przesuwania wzdłuż osi X. Oczywiście nie jest to rozwiązanie idealne. Obracanie obiektami prawym przyciskiem, a kamerą lewym przyciskiem może spowodować pogubienie się obserwatora w aktualnej pozycji obiektów na ekranie. Ruch kamery powinien powodować więc korekty mechaniki przesuwania obiektów, aby cały system nie stracił na intuicyjności, sporo do życzenia pozostawia także płynność odwzorowania ruchu myszki na ruch obiektu. To prawda, ale … cyzelować obroty można prawie w nieskończoność, więc w tym przypadku, z miłosierdzia dla Czytelnika, darujemy sobie dalsze, głębsze zmiany programu. void mouseDragged() { // Funkcja obsługująca przerwanie wywołane przeciągnięciem myszki z wciśniętym klawiszem if (mouseButton==RIGHT){ // Ograniczenie obrotów obiektów do prawego klawisza rotationVector.x=(pmouseY-mouseY); // Przypisanie współrzędnej x wektora obrotu wartości przesunięcia myszki wzdłuż osi X rotationVector.y=(pmouseX-mouseX); // Przypisanie współrzędnej y wektora obrotu wartości przesunięcia myszki wzdłuż osi Y } } Teraz już (oddając cząstkę naszej wolności, w zamian za wygodę) możemy zaimplementować do skryptu zewnętrzną bibliotekę peaesycam. Jak twierdzi jej twórca Jonathan Feinberg biblioteka oferuje „a dead-simple” 😂 rozwiązanie problemu ruchu kamery za pomocą myszki. Mimo swojej prostoty jest bardzo użytecznym narzędziem, a co więcej nie musimy znać jego konstrukcji, aby z niego skorzystać. Aby użyć funkcji oferowanych przez bibliotekę dołączamy ją do skryptu, deklarujemy obiekt (camera) klasy PeasyCam: import peasy.*; PeasyCam camera; , a następnie w sekcji setup() tworzymy obiekt kamery umiejscowionej w odległości 1000 jednostek od środka układu: camera = new PeasyCam(this, 1000); Gotowe. Teraz już można użyć metod zdefiniowanych dla obiektów tej klasy. Ich lista jest dostępna tutaj: peasycam v302 camera.setMinimumDistance(245); camera.setMaximumDistance(1000); camera.lookAt(width/2, height/2, 0, 500); camera.setRightDragHandler(null); camera.setResetOnDoubleClick(false); Wszystkie ustawienia kamery znajdują się w sekcji setup() skryptu. Nie ma potrzeby umieszczać żadnych komend w sekcji draw(). Ponieważ autor biblioteki zadbał o to, żeby wszystkie nazwy metod były równie śmiertelnie proste, co sama biblioteka, chyba zbędne jest ich omawianie. W skrócie, ustawione zostały kolejno: minimalna i maksymalna odległość kamery od obiektu, punkt na który „patrzy” kamera (pamiętajmy o translacji układu!), wyłączenie prawego przycisku myszy (używany jest do obrotów obiektu, wyłączenie resetu kamery (dwukrotne kliknięcie, jak pamiętamy ma resetować obrót obiektu, a nie kamery). Ostatnią rzeczą jaką musimy zrobić to dodać w funkcji obsługującej dwukrotne kliknięcie myszką reset kamery i korektę współrzędnych obiektu, na który patrzy. camera.reset(); camera.lookAt(width/2, height/2, 0, 500); To wszystko. Zbudowaliśmy trójwymiarowy, geocentryczny model układu Ziemia-Słońce. Nadaliśmy mu tekstury, tło i światło. Wprawiliśmy układ w ruch, a następnie umożliwiliśmy jego obserwację pod dowolnym kątem na dwa niezależnie działające sposoby. Całkiem sporo jak na 100 linijek kodu. Działający skończony program prezentuje się następująco: Dla zwiększenia czytelności położenia obiektów dodane zostały elipsy i odcinki pozwalające na lepszą orientację w położeniu Ziemi oraz opisy którym przyciskiem myszy przeciągany jest obraz. Samodzielne dodanie tych elementów nie powinno już w tym miejscu nikomu sprawić trudności. Służą do tego komendy ellipse() i line(). Kod programu: import peasy.*; PeasyCam camera; PMatrix3D MATRIX=new PMatrix3D // Inicjalizacja obiektu MATRIX klasy PMatrix3D (macierz przestrzeni 3D w ujęciu jednorodnym) (1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1); PVector rotationVector= new PVector (0,0,0); // Inicjalizacja obiektu rotationVector klasy PVector (wektor obrotu) int EARTH_RADIUS=150; // Promień Ziemi int SUN_RADIUS=10; // Promień Słońca int SUN_ORBIT=300; // Promień orbity Słońca; int CELESTIAL_SPHERE_RADIUS=4000; // Promień Sfery Niebieskiej float xSol=0; // Chwilowa współrzędna x środka Śłońca float ySol=0; // Chwilowa współrzędna y środka Śłońca float zSol=0; // Chwilowa współrzędna z środka Śłońca float tSol=0; // Chwilowy azymut Słońca liczony od południka 0 w radianach PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemi PImage EARTH_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Ziemi PShape SUN; // Deklaracja kształtu przechowującego informacje o kształcie Słońca PImage SUN_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Słońca PShape CELESTIAL_SPHERE; // Deklaracja kształtu przechowującego informacje o kształcie Sfery Niebieskiej PImage CELESTIAL_SPHERE_TEXTURE; // Deklaracja obrazu przechowującego informacje o teksturze Sfery Niebieskiej void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło smooth(4); // Ustawienie poziomu anty-aliasingu sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); EARTH_TEXTURE=loadImage("1_earth_8k.jpg"); //EARTH_TEXTURE=loadImage("http://shadedrelief.com/natural3/ne3_data/8192/textures/1_earth_8k.jpg"); SUN=createShape(SPHERE, SUN_RADIUS); SUN_TEXTURE=loadImage("320px-Map_of_the_full_sun.jpg"); //SUN_TEXTURE=loadImage("https://upload.wikimedia.org/wikipedia/commons/thumb/9/99/Map_of_the_full_sun.jpg/320px-Map_of_the_full_sun.jpg"); CELESTIAL_SPHERE=createShape(SPHERE, CELESTIAL_SPHERE_RADIUS); CELESTIAL_SPHERE_TEXTURE=loadImage("eso0932a.jpg"); //CELESTIAL_SPHERE_TEXTURE=loadImage("https://cdn.eso.org/images/large/eso0932a.jpg"); EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setTexture(EARTH_TEXTURE); // Przypisanie tekstury kształtowi Ziemi SUN.setStroke(false); // Brak wyświetlania obrysu SUN.setTexture(SUN_TEXTURE); // Przypisanie tekstury kształtowi Słońca CELESTIAL_SPHERE.setStroke(false); // Brak wyświetlania obrysu CELESTIAL_SPHERE.setTexture(CELESTIAL_SPHERE_TEXTURE); // Przypisanie tekstury kształtowi Sfery Niebieskiej camera = new PeasyCam(this, 1000); camera.setMinimumDistance(245); camera.setMaximumDistance(1000); camera.lookAt(width/2, height/2, 0, 500); camera.setRightDragHandler(null); camera.setResetOnDoubleClick(false); } void draw() { background(22); translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu MATRIX.transpose(); // Transpozycja macierzy przestrzeni 3D MATRIX.mult(rotationVector,rotationVector); // Aktualizacja wartości wektora obrotu poprzez przemnożenie go przez macierz przestrzeni MATRIX.transpose(); // Ponowna transpozycja macierzy MATRIX.rotate(TWO_PI/360*6,rotationVector.x,rotationVector.y,rotationVector.z); // Obrót macierzy o kąt 6 stopni wokół zmodyfikowanego wektora x,y,z applyMatrix(MATRIX); // Zastąpienie bieżącej przestrzeni 3D przestrzenią przekształconą 3D rotationVector.set(0,0,0); // Reset wektora obrotu rotateX(TWO_PI/4); // Obrót środka układu współrzędnych o 90 stopni wokół osi X rotateZ(TWO_PI/4); // Obrót środka układu współrzędnych o 90 stopni wokół osi Z pushMatrix(); rotateY(TWO_PI/12); rotateZ(TWO_PI/6); shape(CELESTIAL_SPHERE); popMatrix(); directionalLight(255, 255, 210, -xSol, -ySol, -zSol); // Oświetlenie Ziemi światłem jasnożółtym padającym z kierunku Słońca pushMatrix(); // Wepchnięcie macierzy współrzędnych rotateX(-TWO_PI/4); // Obrót środka układu współrzędnych o -90 stopni wokół osi X rotateY(PI); // Obrót środka układu współrzędnych o 180 stopni wokół osi Y ambientLight(28, 28, 28); // Przyciemnienie Ziemi shape(EARTH); // Wyświetlenie obrazu Ziemi lights(); // Reset ustawień funkcji światła popMatrix(); // Wypchnięcie macierzy współrzędnych xSol=SUN_ORBIT*cos(tSol); // Określenie pozycji X środka Słońca ySol=SUN_ORBIT*sin(tSol); // Określenie pozycji Y środka Słońca tSol+=TWO_PI/360; // Ustalenie azymutu Słońca if (tSol>TWO_PI) tSol=0; // Reset azymutu po zakreśleniu przez słońce pełnej orbity pushMatrix(); // Wepchnięcie macierzy współrzędnych translate(xSol,ySol,zSol); // Przesunięcie środka układu współrzędnych do miejsca położenia Słońca ambientLight(255, 255, 210); // Rozświetlenie Słońca shape(SUN); // Wyświetlenie obrazu Słońca lights(); // Reset ustawień funkcji światła popMatrix(); // Wypchnięcie macierzy współrzędnych } void mouseDragged() { // Funkcja obsługująca przerwanie wywołane przeciągnięciem myszki z wciśniętym klawiszem if (mouseButton==RIGHT){ // Ograniczenie obrotów obiektów do prawego klawisza rotationVector.x=(pmouseY-mouseY); // Przypisanie współrzędnej x wektora obrotu wartości przesunięcia myszki wzdłuż osi X rotationVector.y=(pmouseX-mouseX); // Przypisanie współrzędnej y wektora obrotu wartości przesunięcia myszki wzdłuż osi Y } } void mouseClicked(MouseEvent event) { // Funkcja obsługująca przerwanie wywołane kliknięciem myszki if (event.getCount() == 2) { MATRIX.reset(); // Przywrócenie Ziemi pierwotnego położenia po dwukrotnym kliknięciu myszką camera.reset(); camera.lookAt(width/2, height/2, 0, 500); } } Od Autora Dziękuję wszystkim, którzy dotarli aż do tego miejsca. Jestem pod wrażeniem 🙂 Mam nadzieję, że temat okazał się ciekawy. Przepraszam przy okazji za wszystkie niezręczności w tekście, są praktycznie nieuniknione. Pojawia się pytanie co dalej? Tutaj ograniczeniem jest tylko pojemność kory mózgowej. Można dalej poprawiać program (jest na pewno wieele do ulepszenia, choć przyznam, że jest to najczystszy kod jaki mi osobiście kiedykolwiek udało się napisać, niestety zwykle przypomina śmietnik), można podjąć próbę zasymulowania innego układu po swojemu, można też dodać kolejne obiekty, wyposażyć w działka laserowe, oprogramować kolizje (w sumie ciekawy temat na ew. nowe artykuły) i zaprosić znajomych do własnej kosmicznej strzelaniny (biblioteka: network) w stylu "World of..", a potem ładne to wszystko ubrać i zarobić swój pierwszy 1 000 000$🤔 Czego wszystkim Czytelnikom FORBOTa serdecznie życzę! 😃😃😃
-
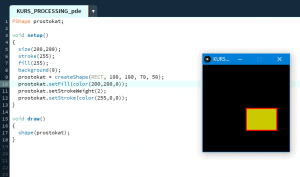
pushMatrix(), popMatrix() Czas na dodanie do programu obrazu Słońca. W poprzedniej części artykułu przedstawione zostały zasady tworzenia obiektów typu PShape. Tworzenie obrazu Słońca dokonywane będzie dokładnie w ten sam sposób co tworzenie obrazu Ziemi. Jedyna różnica polegała będzie na różnicach położenia tych obiektów w układzie współrzędnych. Co więcej, o ile położenie Ziemi będzie stałe, o tyle położenie Słońca będzie się zmieniało w czasie, ponieważ będzie ono krążyło bezustannie wokół Ziemi, a w naszym programie w każdej klatce wyświetlane w nieco innym miejscu. Oczywiście istnieje wiele metod umożliwiających realizację tego zadania, jednak Processing oferuje niezwykle wygodną funkcję pushMatrix(), która w połączeniu ze znanym już translate() znacznie je ułatwia. pushMatrix() zapisuje bieżącą macierz transformacji na stosie danych, a popMatrix() ponownie go stamtąd wydobywa. Transformacje wykonane pomiędzy pushMatrix() a popMatrix() będą dotyczyły układu znajdującego się na stosie. Upraszczając, działanie funkcji pushMatrix() możemy wyobrazić sobie jako wciśnięcie układu współrzędnych razem ze znajdującymi się w nim obiektami w inną rzeczywistość, niż ta która dokonuje się na ekranie. W trakcie przebywania w tej innej rzeczywistości możliwe jest wykonywanie translacji układu współrzędnych oraz operacji na „wciśniętych” razem z nim obiektach. Wywołanie popMatrix() powoduje powrót do poprzedniego układu jednak obiekty pojawiają się w miejscach w jakich znalazły się po dokonaniu translacji poza układem. Dla przykładu narysowanie sfery, a następnie wywołanie funkcji pushMatrix() oraz przesunięcie sfery o 10 jednostek zakończone wywołaniem popMatrix() spowoduje pojawienie się na ekranie obrazu dwóch sfer przesuniętych względem siebie o 10 jednostek, pomimo, że obrazy dotyczą tej samej sfery. Potęga i jednocześnie prostota pushMatrix() jest porównywalna do translate(). Połączenie ich razem jest nieocenionym narzędziem programistycznym. Pojawia się pytanie, gdzie zostanie wyświetlone „Słońce” jeśli nie zostanie przesunięte w odpowiednie miejsce? Oczywiście wewnątrz „Ziemi”, tj. w środku układu współrzędnych. Ponieważ jego promień będzie mniejszy od ziemskiego, nie będzie nawet widoczne. Konieczne jest zatem jego przesunięcie w stosunku do środka współrzędnych oraz wprawienie w ruch wokół Ziemi. Zanim program zostanie odpowiednio zmodyfikowany warto rzucić okiem na stan aktualny, czyli z obrazem Słońca: int EARTH_RADIUS=150; // Promień Ziemi int SUN_RADIUS=10; // Promień Słońca PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemii PShape SUN; // Deklaracja kształtu przechowującego informacje o kształcie Słońca void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło smooth(4); // Ustawienie poziomu anty-aliasingu sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); SUN=createShape(SPHERE, SUN_RADIUS); EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setFill(#0D8FBC); // Kolor wypełnienia #0D8FBC (błękitny) SUN.setStroke(false); // Brak wyświetlania obrysu SUN.setFill(#F5E20A); // Kolor wypełnienia #F5E20A (żółty) } void draw() { translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu shape(EARTH); // Rysunek Ziemi shape(SUN); // Rysunek Słońca } Z punktu widzenia obserwatora na Ziemi Słońce porusza się po nieboskłonie idealnym ruchem okrężnym. Peryhelium i aphelium orbity widoczne może być jako pozorne zmniejszenie lub zwiększenie promienia Słońca, co gołym okiem jest jednak praktycznie niemożliwe. Dlatego w programie przyjęto, że ruch Słońca wokół Ziemi odbywa się po okręgu i nie jest dokonywana korekta promienia gwiazdy. Związane jest to również z faktem, że skala i cykl tej korekty wymaga dość skomplikowanych obliczeń oraz wprowadzania pojęć, które zamieniłyby ten artykuł (i program) w rozprawkę z dziedziny astronomii i astronawigacji. Uwzględniając powyższe ograniczenia, do określenia pozycji słońca względem Ziemi potrzebne będą następujące zmienne: float xSol=0; // Chwilowa współrzędna x środka Słońca float ySol=0; // Chwilowa współrzędna y środka Słońca float zSol=0; // Chwilowa współrzędna z środka Słońca float tSol=0; // Chwilowy azymut Słońca liczony od południka 0 w stopniach int SUN_ORBIT=600; // Promień orbity Słońca Przez chwilowe współrzędne środka słońca należy rozumieć położenie obrazu Słońca w oknie programu w trakcie wyświetlania kolejnych klatek. Chwilowy azymut określa miejsce w jakim znajduje się obraz Słońca względem obrazu ziemskich południków. Współrzędne środka Słońca wyliczane są na podstawie równania okręgu zgodnie z następującym algorytmem: xSol=SUN_ORBIT*cos(tSol); // wyliczenie pozycji x Słońca ySol=SUN_ORBIT*sin(tSol); // wyliczenie pozycji y Słońca tSol+=TWO_PI/360; // inkrementacja azymutu o 1 stopień na klatkę if (tSol>TWO_PI) tSol=0; // reset azymutu po zakreśleniu przez Słońce całej orbity Mając wszystkie niezbędne dane możliwe jest dokonanie odpowiednich przekształceń wykorzystując funkcje popMatrix() oraz translate() pushMatrix(); // wepchnięcie macierzy współrzędnych translate(xSol,ySol,zSol); // przesunięcie środka układu shape(SUN); // wyświetlenie obrazu Słońca popMatrix(); // wypchnięcie macierzy Jak łatwo zauważyć nie została obliczona wartość zmiennej zSol. Nie jest to na tym etapie niezbędne. Ruch Słońca względem osi Z w układzie geocentrycznym wywoływany jest przez nachylenie ekliptyki. Jego określenie wymaga odrębnych, dość zawiłych obliczeń, które nie wnoszą jednak niczego nowego w zakresie opisywanych funkcji, zmniejszając jednocześnie przejrzystość kodu. Tym samym w naszym programie Słońce okrąża Ziemię idealnie w płaszczyźnie równika. Działanie programu uwzględniającego nachylenie ekliptyki zostanie przedstawione na końcu artykułu jako dodatek. Po uzupełnieniu programu o komendy definiujące pozycję Słońca oraz zasady jego wyświetlania pełny kod będzie wyglądał następująco: int EARTH_RADIUS=150; // Promień Ziemi int SUN_RADIUS=10; // Promień Słońca int SUN_ORBIT=300; // Promień orbity Słońca; float xSol=0; // Chwilowa współrzędna x środka Śłońca float ySol=0; // Chwilowa współrzędna y środka Śłońca float zSol=0; // Chwilowa współrzędna z środka Śłońca float tSol=0; // Chwilowy azymut Słońca liczony od południka 0 w radianach float tSolFromSeasonStart=0; // Suma azymutów Słońca w sezonie w okresie obserwacji w radianach PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemii PShape SUN; // Deklaracja kształtu przechowującego informacje o kształcie Słońca void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło smooth(4); // Ustawienie poziomu anty-aliasingu sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); SUN=createShape(SPHERE, SUN_RADIUS); EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setFill(#0D8FBC); // Kolor wypełnienia #0D8FBC (błękitny) SUN.setStroke(false); // Brak wyświetlania obrysu SUN.setFill(#F5E20A); // Kolor wypełnienia #F5E20A (żółty) } void draw() { background(22); // Wymazanie obrazu klatki translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu shape(EARTH); // Rysunek Ziemi xSol=SUN_ORBIT*cos(tSol); ySol=SUN_ORBIT*sin(tSol); tSol+=TWO_PI/360; if (tSol>TWO_PI) tSol=0; pushMatrix(); translate(xSol,ySol,zSol); shape(SUN); popMatrix(); } Po uruchomieniu programu w tej formie otrzymamy następujący obraz: Efekt niesie niemiłą niespodziankę! Słońce zamiast okrążać Ziemię rysuje wokół niej okrąg. Jak już wspomniano, spowodowane jest to faktem, że wpychanie i wypychanie macierzy nie powoduje przesunięcia lub wymazania obrazu obiektów sprzed tej operacji. Widzimy po prostu kolejne obrazy tego samego obiektu, którego przesunięcia odbywają się poza wyświetlaną macierzą współrzędnych. Jedyny sposób, aby temu zaradzić to wyczyszczenie klatki i przerysowanie jej na nowo. Z pomocą przychodzi tu funkcja background(). Jej zastosowanie w pętli draw() będzie powodowało wymazywanie zawartości każdej kolejnej wyświetlanej klatki i rozwiąże problem. background(22); // Wymazanie obrazu klatki Po uzupełnieniu programu o powyższą komendę działa on już zgodnie z oczekiwaniami: Ostatecznie kod przyjmuje postać: int EARTH_RADIUS=150; // Promień Ziemi int SUN_RADIUS=10; // Promień Słońca int SUN_ORBIT=300; // Promień orbity Słońca; float xSol=0; // Chwilowa współrzędna x środka Śłońca float ySol=0; // Chwilowa współrzędna y środka Śłońca float zSol=0; // Chwilowa współrzędna z środka Śłońca float tSol=0; // Chwilowy azymut Słońca liczony od południka 0 w radianach float tSolFromSeasonStart=0; // Suma azymutów Słońca w sezonie w okresie obserwacji w radianach PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemii PShape SUN; // Deklaracja kształtu przechowującego informacje o kształcie Słońca void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło smooth(4); // Ustawienie poziomu anty-aliasingu sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); SUN=createShape(SPHERE, SUN_RADIUS); EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setFill(#0D8FBC); // Kolor wypełnienia #0D8FBC (błękitny) SUN.setStroke(false); // Brak wyświetlania obrysu SUN.setFill(#F5E20A); // Kolor wypełnienia #F5E20A (żółty) } void draw() { background(22); // Wymazanie obrazu klatki translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu shape(EARTH); // Rysunek Ziemi xSol=SUN_ORBIT*cos(tSol); ySol=SUN_ORBIT*sin(tSol); tSol+=TWO_PI/360; if (tSol>TWO_PI) tSol=0; pushMatrix(); translate(xSol,ySol,zSol); shape(SUN); popMatrix(); } W kolejnej, trzeciej części artykułu zajmiemy się światłem i ruchem obserwatora układu (do tej pory układ obserwowany jest z jednego miejsca), a Słońce i Ziemia uzyskają inny, atrakcyjniejszy wygląd. Do tego czasu warto poćwiczyć wykorzystanie funkcji pushMatrix() i popMatrix(). Przy pewnej wprawie stają się one nadzwyczaj użytecznym narzędziem.
-
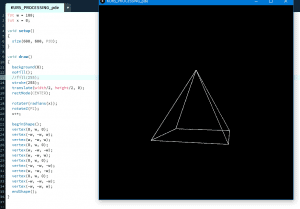
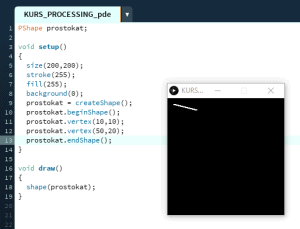
Wstęp W artykule przedstawione zostały wybrane, podstawowe metody operowania obiektami trójwymiarowymi w środowisku Processing 4.0 alpha 3 (rel. 17.01.2021). Pomimo, że zapoznanie się z tematem nie wymaga wcześniejszego doświadczenia z Processing, wskazana jest znajomość fundamentów programowania oraz pewien stopień swobody w budowaniu skryptów. Niekoniecznie w tym środowisku. Prawie wszystkie poruszane tematy uzupełnione są praktycznymi przykładami, składającymi się na kompletny, działający i jednocześnie nieduży program, który następnie może podlegać dalszym modyfikacjom. Co budujemy? W roku 1543 Mikołaj Kopernik opublikował w Norymberdze dzieło, które na zawsze zmieniło postrzeganie Wszechświata. Dzisiaj nie wyobrażamy sobie Układu Słonecznego inaczej niż grupy planet okrążających Słońce. Jednak ujęcie geocentryczne obecne jest w języku potocznym, sztuce, a nawet astronawigacji. Nasz program będzie próbą prezentacji układu Ziemia-Słońce tak, jakby to Ziemia znajdowała się w jego centrum, a nie odwrotnie. Zadaniem programu będzie modelowanie wzajemnego położenia nieruchomej Ziemi (EARTH) i krążącego wokół niej Słońca (SUN). Na koniec dla uatrakcyjnienia całości wprowadzony zostanie również trzeci obiekt: Sfera Niebieska (CELESTIAL_SPHERE). Na potrzeby budowy modelu przyjęto, że zarówno Ziemia jak i Słońce są idealnymi kulami. Założono również, że centrum trójwymiarowego układu współrzędnych, względem którego dokonywane będą przekształcenia, znajduje się w geometrycznym środku Ziemi. Dokonano także uproszczeń mechaniki ruchu Słońca. PShape i translate() Ponieważ program będzie wykorzystywał obiekty i przekształcenia dostępne jedynie w trzech wymiarach naszym pierwszym krokiem będzie ustawienie jednego z 5 dostępnych trybów renderingu na „P3D”. Należy tego dokonać podając trzeci parametr funkcji size() odpowiedzialnej za określenie rozmiarów okna, w którym wykonywany będzie program: size(1800,1000,P3D); // Rozmiar okna 1800/1000 pikseli. Rendering trójwymiarowy Program będzie dokonywał animacji ruchu Słońca wokół Ziemi, czyli sekwencyjnego wyświetlania klatek (frames) zawierających kolejne przekształcenia wzajemnej pozycji tych obiektów. Dlatego zawsze warto mieć na uwadze szybkość z jaką klatki są odtwarzane. Parametrem tym można sterować za pomocą funkcji frameRate(), przy czym domyślną wartością jest 60 fps/s. Na potrzeby programu w zupełności wystarczy 30 fps/s: frameRate(30); // Ilość klatek na sekundę(ftp/s) Ustawienia podstawowych parametrów programu kończą się wyborem koloru tła w skali odcieni szarości: Background(22); // Tło Processing oferuje szereg metod pozwalających na rysowanie obiektów trójwymiarowych. Jednym z wygodniejszych sposobów jest wykorzystanie typu danych PShape pozwalającego na przechowywanie kształtów, w tym kształtów trójwymiarowych. Użycie obiektu przechowującego kształt wymaga jego zadeklarowania: PShape EARTH; // Deklaracja obiektu przechowującego informacje o kształcie Ziemi Od momentu zadeklarowania EARTH jako obiektu typu PShape możliwe będzie wykorzystanie w stosunku do niego wszystkich metod przypisanych do typu PShape. Należy pamiętać, że przed użyciem obiektu musi być on przypisany do kształtu, który z kolei może być wczytany za pomocą funkcji loadShape() lub stworzony funkcją createShape(). Processing oferuje wiele sposobów zastosowania funkcji createShape() oraz zestaw predefiniowanych kształtów wybieranych za pośrednictwem parametrów funkcji. Możliwe jest również grupowanie wielu kształtów oraz wykorzystanie funkcji bez parametrów i zdefiniowanie kształtu później, w trakcie działania programu. W przypadku podania jako parametru kształtu predefiniowanego możliwe jest wykorzystanie w stosunku do niego parametrów kształtu podstawowego. Na przykład w stosunku do predefiniowanego kształtu SPHERE możliwe jest zastosowanie parametrów funkcji sphere(). Aby użyć obiektu EARTH w naszym programie przypisywany jest do niego nowy kształt będący sferą (predefiniowany kształt SPHERE - co zasadniczo odpowiada kształtowi Ziemi) z jednym parametrem określającym jej promień (EARTH_RADIUS). EARTH=createShape(SPHERE,EARTH_RADIUS); // Przypisanie do obiektu EARTH typu PShape predefiniowanego kształtu sfery o zadanym promieniu (jeden z dozwolonych parametrów funkcji podstawowej sphere()) Oczywiście parametr EARTH_RADIUS wymaga wcześniejszego zadeklarowania: int EARTH_RADIUS=150; // Promień Ziemi Samo zadeklarowanie obiektu EARTH i przypisanie do niego zadanego kształtu nie jest wystarczające do jego wyświetlenia. W tym celu konieczne jest użycie dodatkowo funkcji shape(). W programie zastosowano najprostsze jej wywołanie: shape(EARTH); // Rysunek Ziemi Podsumowując, prawidłowe wyświetlenie obiektu typu PShape wymaga: Deklaracji obiektu: PShape Przypisania do obiektu zadanego kształtu: (createShape() lub loadShape()) Wyświetlenia obiektu (wywołania): shape() Sfera w środowisku Processing jest obiektem szczególnym. Ponieważ jej wyświetlenie wymaga narysowania zbioru płaszczyzn, często konieczne jest podjęcie decyzji co do ich liczby, zapewniającej oczekiwane przybliżenie kształtu sfery. Określenie liczby wierzchołków siatki wykorzystywanej do rysowania sfery realizowane jest przez funkcję sphereDetail(). Rozdzielczość domyślna to 30, co pozwala na narysowanie stosunkowo precyzyjnej figury. Przy podejmowaniu decyzji o szczegółowości odtworzenia kształtu należy mieć jednak na uwadze ile sfer będzie rysowanych w tym samym czasie. Im większa liczba użytych płaszczyzn tym mniejsza liczba sfer będzie wyświetlana bez opóźnień wpływających na płynność działania programu. Ponieważ w naszym programie wykorzystywane są tylko 3 sfery możliwe jest ustawienie wysokiego poziomu szczegółowości: sphereDetail(120); // Określenie szczegółowości rysowania sfer Warto pamiętać, aby wywołanie funkcji sphereDetail() odbywało się przed wywołaniem createShape() oraz shape(). Na podstawie zdobytej wiedzy można pokusić się na zbudowanie pierwszej wersji programu, którego zadaniem będzie wyświetlenie sfery o promieniu 150 i szczegółowości 120. Miejsca w których umieszczone są poszczególne komendy nie są przypadkowe! int EARTH_RADIUS=150; // Promień Ziemi PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemii void setup() { // Część programu wykonywana raz size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); } void draw() { // Część program wykonywana w pętli shape(EARTH); // Rysunek Ziemi } Otrzymujemy widok sfery zniekształconej przez perspektywę, której centrum zlokalizowane jest w lewym górnym rogu ekranu. Ponadto, na jej powierzchni widoczne są linie płaszczyzn, z których została zbudowana, a jej kolor daleki jest od koloru Ziemi. Sam rysunek jest też trochę chropowaty. Zacznijmy od naprawienia mankamentów jakimi są kolor i linie na powierzchni obiektu. Jak już wcześniej wspomniano do rysunku Ziemi możliwe będzie wykorzystanie metod przypisanych do typu PShape. Za określenie sposobu wyświetlania koloru obrysu obiektu typu PShape odpowiada metoda setStroke(), natomiast za kolor i wypełnienie kształtu metoda setFill(). W naszym programie określamy je za pośrednictwem dwóch komend: EARTH.setStroke(false); // Ustawienie braku wyświetlania obrysu EARTH.setFill(#0D8FBC); // Kolor wypełnienia #0D8FBC (błękitny) Processing udostępnia wiele sposobów reprezentacji kolorów, które nie zostaną tutaj omówione. Zarówno do prostych jak i zaawansowanych projektów wystarczające jest używanie reprezentacji heksadecymalnej. Wybór żądanego koloru umożliwia wbudowane proste narzędzie „Color Selector” dostępne w menu „Tools”. Dla bardziej wymagających przedsięwzięć wygodniejsze jest jednak korzystanie z zewnętrznych narzędzi wyboru koloru. Za „chropowatość” linii odpowiada zjawisko aliasingu. Standardowo w trybie renderingu P3D anty-aliasing ustawiony jest na poziom 2x. W zależności od wydajności sprzętu możliwe jest zastosowanie wygładzania z poziomem 4x lub 8x. W programie zastosowano poziom 4, czyli czterokrotny poziom nadmiaru próbkowania bufora grafiki. smooth(4); // Ustawienie poziomu anty-aliasingu Ponieważ Ziemia znajduje się w centrum uwagi naszego programu konieczne jest na koniec nadanie należnego jej miejsca. W tym celu można, choć nie jest to jedyny sposób, wykorzystać niezwykle potężną funkcję translate(). W środowisku 3D translację można wyobrazić sobie jako przesunięcie środka układu współrzędnych x,y,z o zadaną wartość wzdłuż poszczególnych osi. Z funkcji należy korzystać bardzo ostrożnie. Przekształcenia geometryczne są wrażliwe na kolejność w jakiej wywoływane będą poszczególne funkcje. W konsekwencji narysowanie obiektu np. w środku układu współrzędnych, a następnie zastosowanie funkcji translate() nie spowoduje jego przesunięcia. Pozostanie on tam gdzie został pierwotnie narysowany, przesunie się natomiast sam układ współrzędnych. Przy okazji należy pamiętać, że w środowisku trójwymiarowym Processing, układ współrzędnych jest lewoskrętnym układem kartezjańskim, którego środek umiejscowiony jest w lewym górnym rogu ekranu. Wartości Y rosną w kierunku dołu ekranu, wartości X w kierunku prawej strony ekranu, natomiast wartości Z zwiększają się w kierunku ruchu do powierzchni ekranu i zmniejszają w kierunku w „głąb” ekranu. Do tej pory nie wskazano gdzie dokładnie ma zostać wyświetlona Ziemia. W konsekwencji została ona umieszczona przez program w środku układu współrzędnych, który znajduje się jak wspomniano w lewym górnym rogu ekranu. Aby przesunąć ją w docelowe miejsce konieczne jest przesunięcie środka układu współrzędnych do centrum okna programu. translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu W tym konkretnym przypadku zamiast bezpośredniego podania przesunięcia wzdłuż osi X oraz osi Y wykorzystano zmienne systemowe height oraz width przechowujące rozmiary okna programu zdefiniowane na poziomie funkcji size(). W konsekwencji środek układu współrzędnych przesunął się o połowę szerokości okna wzdłuż osi X oraz połowę wysokości okna wzdłuż osi Y, nie zmieniając swojego położenia na osi Z. Po dokonaniu powyższych modyfikacji program przyjął następującą formę: int EARTH_RADIUS=150; // Promień Ziemi PShape EARTH; // Deklaracja kształtu przechowującego informacje o kształcie Ziemii void setup() { size(1800,1000,P3D); // Rozmiar okna 1800/1000 pixeli. Rendering trójwymiarowy frameRate(30); // Ilość klatek na sekundę(ftp/s) background(22); // Tło sphereDetail(120); // Szczegółowość rysowania sfer EARTH=createShape(SPHERE,EARTH_RADIUS); smooth(4); // Ustawienie poziomu anty-aliasingu EARTH.setStroke(false); // Brak wyświetlania obrysu EARTH.setFill(#0D8FBC); // Kolor wypełnienia #0D8FBC (błękitny) } void draw() { translate(width/2,height/2,0); // Przesunięcie środka układu współrzędnych do centrum ekranu/okna programu – kolejność jest ważna! shape(EARTH); // Rysunek Ziemi } W centrum okna wyświetlana jest gładka, niebieska sfera: W tym miejscu kończy się Część Pierwsza. Przed sięgnięciem do Części Drugiej, gdzie do programu dodamy funkcje odpowiedzialne za Słońce oraz jego obrót wokół Ziemi, a obrazy sfer zostaną nieco bardziej urealnione, zachęcam do eksperymentów z różnymi obiektami typu PShape i funkcją translate().
-
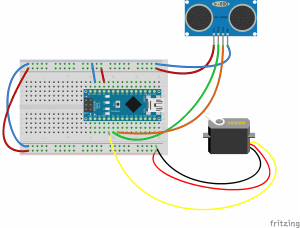
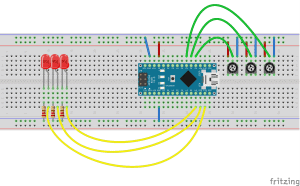
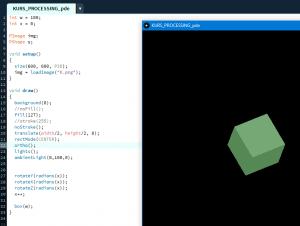
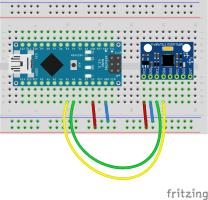
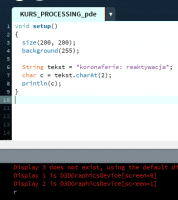
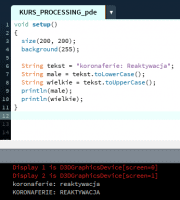
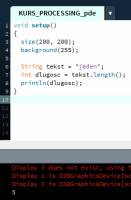
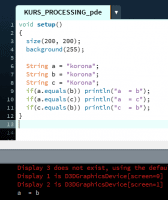
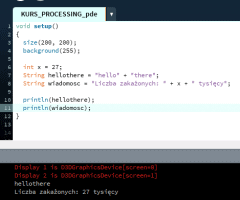
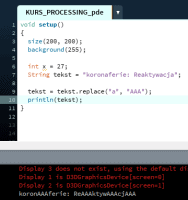
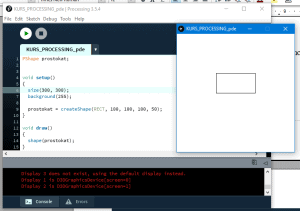
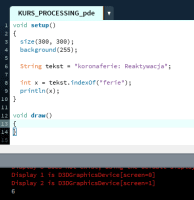
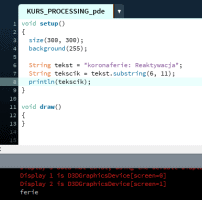
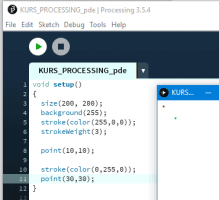
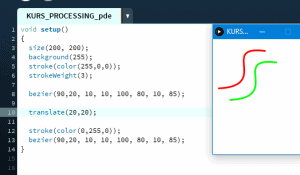
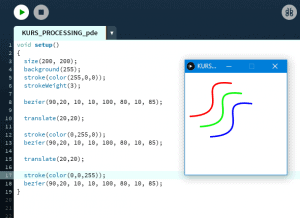
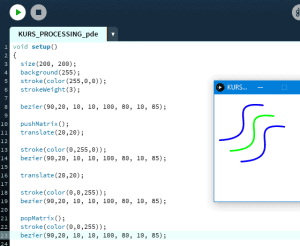
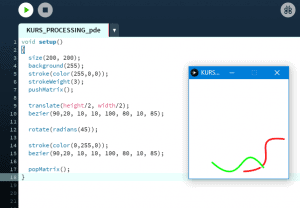
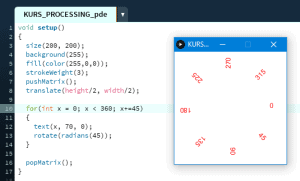
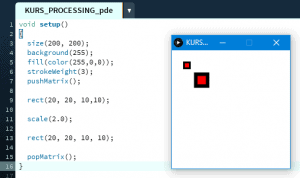
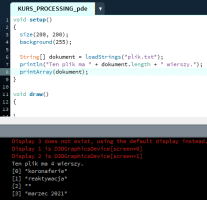
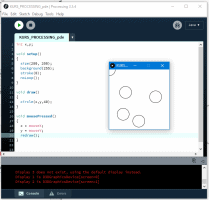
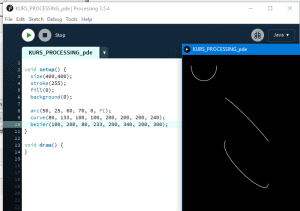
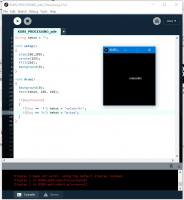
Ten artykuł jest częścią serii "Kurs programowania w Processing" #1 - Wstęp, kształty, debugger #2 - Piksele 2D oraz interaktywność #3 - Tekst, pliki, dźwięk, przekształcenia #4 - OpenGL, Arduino! Czy kiedykolwiek miałeś potrzebę podłączenia Arduino z komputerem? Pokazać dane z czujników w efektowny i czytelny sposób? A może zrobić z komputera panel sterowania do nowego robota? Albo po prostu pobawić się obrazem i dźwiękiem - do tego wszystkiego bowiem, możemy wykorzystać środowisko o nazwie Processing. Czym jest Processing? logo programu Processing Krótko mówiąc, Processing to język programowania wraz z IDE, podobnie jak Arduino. Różnica jest taka, że zamiast fizycznej płytki dostajemy własne okienko, "płótno", po którym możemy rysować, klikać, co tylko zechcemy. Jedni wykorzystują to do projektowania interfejsu dla urządzeń (np. popularny projekt radaru na HC-SR04), drudzy wykorzystują to do tworzenia sztuki elektronicznej. Prostota języka i łatwość debugowania zachęca wielu ludzi do skorzystania z tego narzędzia. Ten artykuł bierze udział w naszym konkursie! 🔥 Na zwycięzców czekają karty podarunkowe Allegro, m.in.: 2000 zł, 1000 zł i 500 zł. Potrafisz napisać podobny poradnik? Opublikuj go na forum i zgłoś się do konkursu! Czekamy na ciekawe teksty związane z elektroniką i programowaniem. Sprawdź szczegóły » Dlaczego Processing? Jak już wspomniałem, przede wszystkim Processing jest łatwy i intuicyjny, a składnia jest podobna do C++, jak Arduino. Samo środowisko jest oparte o Javę, więc aplikacja może bez problemu zadziałać zarówno na Windowsie, jak i na Linuxie. Aplikacje napisane w Processingu można nawet skompilować do pliku wykonywalnego, aby uruchamiać ją "samodzielnie". Okienko, które jest naszym płótnem, może wyłapywać wejście z klawiatury, myszki, komunikować się z Arduino, obsługiwać pliki, dźwięk, a przede wszystkim, cały projekt jest objęty licencją GPL (opensource)! Wszystkie te czynniki przemawiają za Processingiem, a szczególnie dla hobbystów. Co mogę zrobić używając Processingu? Tutaj, podobnie jak w przypadku Arduino, ogranicza nas tylko wyobraźnia. Radar, panel sterujący, analizator stanów logicznych, czy kalkulator funkcji kwadratowej - wszystko zależy od nas. Także program ten może się przydać i do tworzenia aplikacji, i do animacji, i symulacji, dla hobbystów, nauczycieli i uczniów, a przede wszystkim - dla Ciebie! Środowisko Plik instalacyjny pobieramy z tej strony. Wybieramy odpowiedni system, pobieramy i instalujemy - po krótkim czasie, przywita nas okienko z nowym szkicem: Wygląda znajomo, prawda? Cóż, tak działa magia oprogramowania rozpowszechnianego na licencji GNU GPL. Arduino IDE jak widać mocno bazuje na IDE Processingu, co dla ludzi którzy wcześniej korzystali z Arduino IDE tylko ułatwi sprawę. Tak więc podobnie jak Arduino IDE, Processing składa się głównie z okna edytora tekstu, konsoli na dole, przycisku “Uruchom” i “Stop”. Konsolę możemy przełączać także z listą błędów i ostrzeżeń. Te będą się pojawiać jeszcze przed skompilowaniem, co pozwoli zaoszczędzić trochę czasu: W pasku na górze, warto zwrócić uwagę na opcję wyeksportowania programu (File > Export Application), debugera (o którym za chwilę), narzędziami. Do omówienia zostały opcje po prawej: Przycisk z “motylkiem” włączy debuger. Pozwoli on podejrzeć nam, jak działa program, a co za tym idzie – o wiele szybciej wyłapać potencjalny błąd. Zakładka “Java” pozwala wybrać moduł processingu, ponieważ samo IDE pozwala na wiele więcej: Wielu opcji niestety nie omówię w kursie, ale warto wiedzieć, że szkice w Processingu mogą być uruchamiane w przeglądarce (p5.js), można edytować shadery, tworzyć aplikacje pod Androida czy w języku R. Także po omówieniu IDE – pora napisać pierwszy program. A może od razu by tak nacisnąć przycisk “Start”... ? Po uruchomieniu “pustego” programu, dostaliśmy puste okienko... także w przeciwieństwie do Arduino, nie są wymagane funkcje setup() i loop(), chociaż zaraz użyjemy ich odpowiedników: void setup() { size(200, 200); stroke(0); background(255); circle(100, 100, 40); } Tak więc – funkcja setup() wykonuje się raz na początku programu, tak jak w Arduino. Najczęściej będziemy w niej inicjalizować pewne rzeczy, w tym przypadku - kolor tła i kreski. Zdefiniowaliśmy także rozmiar okna programu, który powinniśmy zawsze dawać na początku programu. size(x, y); zmieni rozmiar ekranu na szerokość (x), i wysokość (y), w pikselach. stroke(w); zmieni kolor kreski, którą rysujemy kształty. “w” określi intensywność w skali czarnobiałej (0 to czarny, 255 to biały). background(w); działa podobnie do wyżej opisanej funkcji, tylko że zmienia kolor tła. Warto nadmienić, że zamiast "w" możemy dać 3 wartości "r", "g", "b" (a czasem nawet "a"), aby uzyskać kolorowy odcień: background(0, 255, 0); //background(r, g, b), tutaj będzie kolor zielony stroke(255, 0, 0); //stroke(r, g, b), tutaj będzie kolor czerwony Ostatni wiersz: circle(x,y,fi); narysuje nam koło ze środkiem w x, y – WAŻNE: układ współrzędnych zaczyna się od lewego, górnego rogu ekranu. Pierwszym pikselem zawsze jest 0,0 (górny, lewy róg) – a ostatni piksel, w dolnym, prawym rogu okna, będzie 199,199, czyli szerokość i wysokość ekranu – 1 (ponieważ liczymy od zera)! "fi" jest średnicą koła (technicznie rzecz biorąc, wysokością i szerokością elipsy). Tak więc, po uruchomieniu powyższego programu, powinniśmy otrzymać nasz czarny okrąg: Zaledwie 6 linijek kodu, a już mamy pierwszy obraz! Spróbujmy zatem dodać ruch do tego obrazka – ot, żeby nasze koło śledziło nasz kursor. Do tego potrzebujemy kolejną funkcję draw(), która jest wykonywana co wyrenderowaną (narysowaną) klatkę naszego okienka (odpowiednik loop() w Arduino). Z racji tego że chcemy co klatkę narysować nowe koło, przenosimy tą funkcję do draw(): void setup() { size(200, 200); stroke(0); background(255); } void draw() { circle(mouseX, mouseY, 40); } "mouseX" oraz "mouseY" są “wbudowanymi” zmiennymi w Processingu, nie trzeba ich deklarować czy zmieniać, po prostu są dostępne “od ręki”. Processing udostępnia więcej takich zmiennych, o czym powiem w dalszej części kursu. Także co narysowaną klatkę rysujemy nowe koło, ze środkiem tam, gdzie aktualnie przebywa nasz kursor. Efekt jest dość ciekawy: Tylko dlaczego mamy tyle kółek? Cóż, co funkcję rysujemy nowe koło, które się nakłada na “stare”. Możemy temu zapobiec, np. czyszcząc ekran co nową klatkę: void setup() { size(200, 200); stroke(0); } void draw() { background(255); circle(mouseX, mouseY, 40); } Powinniśmy mieć teraz tylko jedno koło śledzące nasz kursor: Spróbuj teraz napisać program, który będzie rysował koło tam gdzie jest kursor, i zmieniał odcień koloru w zależności od wysokości myszki, np. Odcień czerwonego: (na razie nie trzeba się przejmować że pozycja kursora będzie większa od 255, ponieważ okno programu jest mniejsze od 255x255px.) W razie problemów, nie bój się spytać o pomoc w komentarzu! Nadmienię też, że w Processingu możemy napisać "println" i "print", aby wyświetlić tekst w konsoli. Jest to tutaj mniej przydatna funkcja, ale niektórym osobom przesiadającym się z Arduino na pewno się przyda: Przechodząc dalej, koła możemy rysować na wiele różnych sposobów, i może trochę profesjonalniej, bo funkcją pozwalającą rysować także elipsy: ellipse(x, y, szerokość, wysokość); stworzy elipsę ze środkiem w x, y od lewego górnego rogu ekranu, o podanej wysokości i szerokości. Ale! Jeżeli przed narysowaniem elipsy wywołamy ellipseMode(CORNER); wtedy x i y będą koordynatami górnego lewego rogu prostokąta, w który elipsa ta jest wrysowana. Jeżeli mamy koordynaty dwóch rogów – lewego górnego, i dolnego prawego, możemy na ich podstawie także narysować elipsę, wykorzystując ellipseMode(CORNERS); wtedy funkcja rysująca przyjmie formę: ellipse(x1, y1, x2, y2); Ale elipsy nie są jedynymi kształtami które można rysować – do dyspozycji mamy przede wszystkim punkt (piksel): point(x, y); narysuje nam piksel w koordynatach x i y. line (x1, y1, x2, y2); narysuje nam linię z początkiem w punkcie A(x1, y1), a kończąc na punkcie B(x2, y2). I oczywiście prostokąt: rect(x, y, szerokość, wysokość); I tutaj, ważne, domyślnie będzie on rysowany od lewego górnego rogu, w przeciwieństwie do elipsy, która była rysowana domyślnie od środka. Możemy to zmienić wykonując rectMode(CENTER), wtedy x i y będą koordynatami symetrycznego środka prostokąta. I podobnie jak z elipsą, możemy podać dwa rogi prostokąta: rectMode(CORNERS); rect(x1,y1,x2,y2); Co więcej, jak dotąd zmienialiśmy kolor kreski, używając stroke(). Możemy także zmienić wypełnienie, używając fill()! Debuger Processing pozwala także na debugowanie programu. W praktyce pozwala on nam uruchamiać program w krokach, oraz podejrzeć wartości zmiennych. Także sprawdźmy, jak zachowa się poniższy, przykładowy program podczas takiego debugowania: int zmienna = 0; void setup() { size(200, 200); stroke(0); } void draw() { println(zmienna); background(255); circle(mouseX, mouseY, 40); zmienna++; } Kroki w których program się "zatrzymuje" możemy ustawiać klikając na numer wiersza: Aby odznaczyć dany wiersz, możemy kliknąć ponownie na numer. Chociaż o wiele wygodniej będzie to robić skrótem klawiszowym, Ctrl+B, przełączającym dany wiersz. Aby uruchomić debuger, klikamy na przycisk "motylka": Pojawiło nam się nowe okienko: to okienko będzie dla nas bardzo ważne, ponieważ tam się będą wyświetlać wszystkie zmienne i parametry naszego programu. Aby sprawdzić czy wszystko działa, ustawiłem "breakpoint" w wierszu 12: Teraz zostało nam uruchomić program. Jak widzimy, pojawiło się okienko naszego programu, lecz szare. Co więcej, okienko ze zmiennymi "zapełniło" się nowymi wartościami, a zamiast rombu przy wierszu 12 – widnieje trójkąt. I wszystko idzie tak, jak chcemy: nasz program przerwał wykonywanie przed wierszem 12 – czyli pokolorowaniem tła na biało. W okienku ze zmiennymi widać naszą zmienną, "zmienna", na razie o wartości 0. Trójkącik przy linijce oznacza, że przy niej zatrzymał się program. Aby kontynuować jego działanie, wystarczy kliknąć "Continue", lub Ctrl+U: Warto zaznaczyć, że obok przycisku "Continue" jest przycisk "Step". Pozwala on na kontynuowanie programu, ale nie do następnego "breakpointa", a tylko do następnej linijki. Naciskając ciągle ten przycisk, uruchomimy program linijka po linijce. Po chwili zabawy debugerem możemy zauważyć, że nasza zmienna się zwiększyła: Specjalnie dodałem także "println" w programie, żeby pokazać, że debuger jest lepszym rozwiązaniem od takiego "manualnego" debugowania, które pewnie wielu z nas stosowało w Arduino: Debuger jest po prostu bardziej czytelny i przyjaźniejszy, pozwala kontrolować program na bierząco. Na pewno też już każdy rozwinął "folder" o nazwie Processing w okienku ze zmiennymi. Zawierają się tam wszystkie zmienne "systemowe" naszego środowiska: Znajdują się tam także wartości mouseX i mouseY, które wykorzystujemy w naszym programie, a także wiele innych zmiennych, które omówimy później. Tak wygląda wstęp do programowania w Processingu, który jak widać, nie jest taki trudny. W następnej części omówimy szerzej interakcje z użytkownikiem, oraz więcej funkcji dot. Rysowania w 2D. Do czasu opublikowania następnej części proponuję w formie ćwiczenia napisać program, który będzie symulował odbijającą się piłeczkę:
-

Kurs programowania w Processing - #4 - OpenGL, Arduino!
Leoneq opublikował temat w Artykuły użytkowników
Ten artykuł jest częścią serii "Kurs programowania w Processing" #1 - Wstęp, kształty, debugger #2 - Piksele 2D oraz interaktywność #3 - Tekst, pliki, dźwięk, przekształcenia #4 - OpenGL, Arduino! Po miesiącu oczekiwania, w końcu połączymy świat rzeczywisty ze światem wirtualnym - albowiem połączymy dzisiaj Arduino wraz z Processingiem, robiąc razem 3 projekty. Ten artykuł bierze udział w naszym konkursie! 🔥 Na zwycięzców czekają karty podarunkowe Allegro, m.in.: 2000 zł, 1000 zł i 500 zł. Potrafisz napisać podobny poradnik? Opublikuj go na forum i zgłoś się do konkursu! Czekamy na ciekawe teksty związane z elektroniką i programowaniem. Sprawdź szczegóły » Zacznijmy od prostego scenariuszu: posiadamy urządzenie oparte o Arduino (lub inną płytkę), i dane z tego urządzenia chcemy wykorzystać w processingu - czy to do wyświetlenia ich, odczytania i zapisania w pliku, czy aktualizacji ich w bazie danych. Do połączenia takiego Arduino z komputerem posłuży nam (wirtualny) port szeregowy, znany z konsoli w Arduino IDE. Ogólnie rzecz biorąc - i co było w kursie Arduino - będziemy się komunikować przez UART, czyli będziemy wysyłać (tutaj) ośmiobitowe bajty. Informacja ta będzie dla nas bardzo ważna, gdy przejdziemy do kodowania. Ale, kontynuując: zrobimy sobie właśnie takie urządzenie, z którego dane będą wysyłane do Processingu w przystępnej formie. Zbudujemy sobie dość znany projekt radaru ultradźwiękowego. Składniki: czujnik HC-SR04 płytka z mikrokontrolerem (Arduino, ESP, Nucleo) konwerter usb - uart, jeżeli nasza płytka takiego nie posiada serwo SG90 lub inne cyfrowe przewody połączeniowe, płytka stykowa. Prosiłbym o zignorowanie wyświetlacza, pierwotnie miał zostać użyty, lecz po badaniu wśród znajomych uznałem że nie wszyscy mogą takowy mieć. Jeżeli taki jednak masz, nie krępuj się go dodać! Całość łączymy zgodnie ze schematem: Przykładowe wykonanie może wyglądać tak. Wydrukowałem uchwyt czujnika do serwa (równie dobrze można przykleić taśmą), a samo serwo przykleiłem przez taśmę do stołu. Przed kodowaniem, rozpiszmy sobie co chcemy osiągnąć, na razie na samym Arduino. Mikrokontroler powinien czekać na znak od komputera, zanim zacznie skanowanie. Skanować powinien co jeden stopień, a następnie dane o rotacji i zmierzonej odległości przesłać do Processingu. Tak więc; zaczynamy od zaimportowania potrzebnych bibliotek. Potrzebujemy biblioteki od serwa, i użytkownicy Plaftormio IDE muszą dodać bibliotekę Arduino. #include <Arduino.h> #include <Servo.h> Następnie zdeklarujmy serwo, oraz 2 zmienne, przechowujące kąt obrotu, oraz jego kierunek. Servo serwo; byte obrot = 0; bool kierunek = true; Z racji tego że serwo będziemy obracać w zakresie 0-180 stopni, nie musimy użyć zmiennej typu int tylko byte - warto pamiętać o takiej optymalizacji, ponieważ pozwoli nam to wcisnąć więcej kodu przy rozbudowanych programach. Aby program uczynić uniwersalnym, zdefiniujmy piny: #define PIN_SERVO 2 #define PIN_ECHO 4 #define PIN_TRIG 3 Następnie przechodzimy do funkcji setup(). Przede wszystkim musimy rozpocząć komunikację UART, podłączyć serwo i piny czujnika. Serial.begin(115200); serwo.attach(PIN_SERVO); pinMode(PIN_ECHO, INPUT); pinMode(PIN_TRIG, OUTPUT); Pozostało nam jedynie poczekać, aż dostaniemy znak od komputera aby rozpocząć pracę. Jest na to dość prosty trik: while(Serial.available() > 0) Serial.read();// czyscimy bufor while(!Serial.available()); // czekamy while(Serial.available() > 0) Serial.read(); // czyscimy bufor znowu Najpierw w pętli while czyścimy bufor wejściowy, odczytując to co tam może siedzieć. Środkowa pętla while() będzie blokowała cały program, dopóki nie dostanie jakiegokolwiek znaku od komputera. Po odebraniu takowego, czyścimy bufor znowu - aby nie zaśmiecić go przypadkiem, co potem mogłoby spowodować błąd programu. W funkcji loop() chcemy obracać serwo. Obróćmy je zatem: serwo.write(obrot); Aby jednak obracało się ono o 180 stopni, powinniśmy dodać kod który w zależności od kierunku - dodaje lub odejmuje stopień. if(kierunek) obrot++; else obrot--; if(obrot >= 180) kierunek = 0; if(obrot <= 0) kierunek = 1; Następnie chcemy wykonać pomiar czujnikiem. Chcemy go także wysłać do komputera, pytanie w jakiej formie? Zwykłe wysłanie dwóch liczb nie będzie działało zbyt dobrze. Spróbujemy zrobić zatem "pakiet" danych, zbudowany z nagłówka, oraz samych danych. Serial.print("ok:\t"); Serial.print(zmierz()); Serial.print("\t"); Serial.println(obrot); Dane jakie wysyłamy zaczynają się od "ok:". Oczywiście, każdy może sobie zacząć jak chce; dla mnie oznacza to skrót od obrót i kąt. Znak \t to tabulator - dla programu to może być inny, jak spacja czy znak nowej linii, lecz tabulator pozwala na czytelne podejrzenie danych w konsoli - jak ktoś nie wierzy, może sam sprawdzić. Ostatni wiersz wysyła jeszcze znak nowej linii, który nam powie że to koniec pakietu. Żeby wszystko działało stabilnie (dać czas na pomiar i obrót serwa) do pętli możemy dodać małego delaya. delay(5); No i oczywiście, wysyłamy zmienną zmierz() typu int. Napiszmy zatem co ona zwraca. Jest to kod wzięty bezpośrednio z kursu Arduino, więc myślę że działanie jest jasne. int zmierz() { int czas = 0; int dystans = 0; digitalWrite(PIN_TRIG, LOW); delayMicroseconds(2); digitalWrite(PIN_TRIG, HIGH); delayMicroseconds(10); digitalWrite(PIN_TRIG, LOW); czas = pulseIn(PIN_ECHO, HIGH); dystans = czas / 58; return dystans; } Także cały program powinien wyglądać mniej więcej (z naciskiem na więcej) tak: (dodałem tylko kilka komunikatów i komentarzy) #include <Arduino.h> #include <Servo.h> Servo serwo; byte obrot = 0; bool kierunek = true; #define PIN_SERVO 2 #define PIN_ECHO 4 #define PIN_TRIG 3 int zmierz() { int czas = 0; int dystans = 0; digitalWrite(PIN_TRIG, LOW); delayMicroseconds(2); digitalWrite(PIN_TRIG, HIGH); delayMicroseconds(10); digitalWrite(PIN_TRIG, LOW); czas = pulseIn(PIN_ECHO, HIGH); dystans = czas / 58; return dystans; } void setup() { Serial.begin(115200); Serial.println("Inicjalizacja radaru..."); Serial.println("Inicjalizuje serwo."); serwo.attach(PIN_SERVO); Serial.println("Inicjalizuje czujnik ultradzwiekowy."); pinMode(PIN_ECHO, INPUT); pinMode(PIN_TRIG, OUTPUT); Serial.println("Czekam na dowolny znak aby rozpoczac dzialanie."); while(Serial.available() && Serial.read()); // czyscimy bufor while(!Serial.available()); // czekamy while(Serial.available() && Serial.read()); // czyscimy bufor znowu } void loop() { if(kierunek) obrot++; else obrot--; if(obrot >= 180) kierunek = 0; if(obrot <= 0) kierunek = 1; serwo.write(obrot); Serial.print("ok:\t"); Serial.print(zmierz()); Serial.print("\t"); Serial.println(obrot); delay(5); } Możemy teraz wgrać kod do Arduino, i przystąpić do pisania programu docelowego. Patrząc na radary w wyszukiwarce, chcemy utworzyć półkole w którym będziemy rysować odległości. Jednak! Chcemy przecież pracować z portem szeregowym - na sam początek skryptu musimy zatem dodać bibliotekę od tego. Jest ona domyślnie zainstalowana. Tworzymy od razu port szeregowy port. import processing.serial.*; Serial port; Następnie tworzymy zmienne przechowujące odebrane dane. Ja sobie jeszcze stworzyłem zmienną pomocniczą do rysowania samego radaru. float obrot = 0; float odleglosc = 200; int liczbaPolkoli = 5; W funkcji setup, standardowo definiujemy okienko, oraz jego wielkość. Tworzymy nowy port szeregowy (znowu wchodzi tutaj składnia javy, więc może być ciężko): void setup() { size(800, 600); port = new Serial(this, "COM1", 115200); background(0); } Port COM zastępujemy naszym portem w Windowsie, lub /dev/tty w linuxie. Jeżeli nie wiemy gdzie mamy nasze urządzenie, możemy to sprawdzić w menedżerze urządzeń, lub tym prostym kodem: printArray(Serial.list()); Wypisze on w konsoli listę dostępnych portów. Przechodząc do funkcji draw() - zaczynamy od zapamiętania obecnego położenia okna, i ustawienia środka układu współrzędnych w prawie że centrum okienka. Pozwoli to nam na bardzo łatwe i przyjemne narysowanie wykresu. Zamiast wartości 100 jednak lepiej byłoby wpisać wyliczoną wartość, np. height/6. pushMatrix(); translate(width/2, height-100); Następnie definiujemy pozostałe rzeczy potrzebne do narysowania interfejsu: strokeWeight(2); noFill(); stroke(0,127,0); textAlign(CENTER); Teraz możemy przejść do właściwego narysowania całości. Chcemy osiągnąć efekt podobny do tego: Zaczynamy zatem od narysowania linii poziomej wzdłuż osi X. Następnie liczmy zmienną pomocniczą, określającą promień najmniejszego półkola - pozostałe będą miały promień jego wielokrotności. Znowu, dodałem mały, stały margines - który także powinien zostać wyliczony, w celu zachowania responsywności. line(-width/2,0,width/2,0); float promien = (width-50)/liczbaPolkoli; Teraz musimy się zastanowić, jak tutaj narysować 5 półkoli i się nie namęczyć. Chcemy na pewno zrobić to w pętli for. Chcemy także zastosować arc(), bo chcemy mieć połówkę koła, a nie stricte krzywą. Przydałoby się też narysować odległości, bo w końcu od tego mamy te półkole - żeby pozwoliły nam oszacować odległość. for(int i = 1; i <= liczbaPolkoli; i++) { arc(0,0, promien*i, promien*i, PI, TWO_PI); // domyślnie, czyli od srodka } Ta pętla nam narysuje same półkola. Zauważ, że zaczynamy ją od 1 a nie 0; w końcu chcemy narysować 5 półkoli, a nie 4. Środek prostokąta, w który jest wrysowany nasz wycinek koła, znajduje się dokładnie w punkcie 0, 0. Szerokość i wysokość będą te same, jak mówiłem, wyliczony promień i jego wielokrotności. Następnie, z racji tego że po prawej stronie mamy 0 stopni, to chcemy wyświetlić wycinek od π radianów (180 stopni) do 2π radianów (360 stopni). Jednak aby narysować tekst, no, trzeba byłoby się nagimnastykować. Trzeba go usadowić odpowiednio względem półkola, obliczyć jego wysokość, odległość... lub możemy przesunąć całą siatkę. for(int i = 1; i <= liczbaPolkoli; i++) { arc(0,0, promien*i, promien*i, PI, TWO_PI); // domyślnie, czyli od srodka pushMatrix(); translate(promien*i/2, 20); fill(0,127,0); text(map(promien*i,0,width,0,200), 0,0); noFill(); popMatrix(); } Musimy teraz narysować linie pokazujące obecny kąt. Chcemy ich 5, od 150 do 30 stopni co 30 stopni. Zrobimy więc taką samą pętlę for, ale... tutaj jednak trzeba trochę pokombinować. Między pętlami obracam całą siatkę o 210 stopni, czyli linia będzie narysowana na 150 stopniach. Skoro obracamy całą siatkę, to po prostu rysujemy linię wzdłuż osi Y. //... popMatrix(); } rotate(radians(210)); for(int i = 1; i <= 5; i++) { line(0,0,width/2,0); Następnie ponownie przesuwamy siatkę aby narysować tekst. Obracam jeszcze całość o 90 stopni, inaczej tekst także narysowałby się wzdłuż osi Y. pushMatrix(); translate(width/2+10, 0); rotate(radians(90)); fill(0,127,0); text(180 - (i*30) + "°", 0, 0); noFill(); popMatrix(); Na końcu pętli wystarczy jeszcze dopisać obrót o 30 stopni. Po wykonaniu się całości, siatka się obróci o 210 + 5 * 30 = 360 stopni, czyli "wróci do domu". for(int i = 1; i <= 5; i++) { line(0,0,width/2,0); pushMatrix(); translate(width/2+10, 0); rotate(radians(90)); fill(0,127,0); text(180 - (i*30) + "°", 0, 0); noFill(); popMatrix(); rotate(radians(30)); } Zostało nam narysować samą linię radaru. stroke(0,255,0); pushMatrix(); rotate(PI + radians(obrot)); line(0,0,width/2,0); stroke(255,0,0); line(constrain(odleglosc*2, 0, 200),0,width/2,0); popMatrix(); Znowu obracamy siatkę, tym razem o kąt odczytany z Arduino. Rysujemy zieloną linię (stroke 0,255,0), oraz czerwoną (stroke 255,0,0). Pierwszy punkt powinien być odsunięty o odległość, ja jeszcze przemnożyłem to x2 aby efekt był lepiej widoczny. Program jak widać jest prosty, kilka przekształceń siatki i tyle. Jak szukałem niegdyś gotowych projektów, to jak ludzie się trudzili; funkcje trygonometryczne; twierdzenie talesa, pitagorasa... Należy zatem zawsze szukać najprostszej drogi, i dążyć do optymalizacji. Na końcu pętli zostało nam wrócić do lewego górnego rogu, oraz - aby linie się nie nakładały, możemy albo zrobić co klatkę nowe tło (background), lub narysować półprzezroczysty prostokąt. popMatrix(); //wracamy do lewego gornego rogu //symulujemy zanik linii noStroke(); fill(0,4); rect(0,0,width,height); } Taki prostokąt da bardzo przyjemny efekt. Jeżeli cały obraz mamy gotowy do rysowania, to możemy przystąpić do omówienia kwestii połączenia z Arduino. Zacznijmy od napisania prostej funkcji, wysyłającej do płytki ten "znak", że ma zacząć pracę - i to dosłownie: void keyPressed() { port.clear(); port.write('f'); } Po naciśnięciu dowolnego klawisza zostanie wysłany znak, rozpoczynający pracę. Przed wysłaniem jedynie czyścimy profilaktycznie bufor. Zostało teraz odczytywać dane z Arduino. Za każdym razem, kiedy coś przychodzi do komputera, wykonuje się funkcja serialEvent. Podajemy jej tylko argument, port, wskazujący konkretnie z jakim portem mamy do czynienia. W środku, podobnie jak w Arduino, odczytujemy bufor: void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt != null) println(odczyt); else return; } Tylko tyle wystarczy, aby wypisać co tam nam Arduinen wysyła. Jednak my chcemy jeszcze odczytać wartości z naszego pakietu, i przypisać je do zmiennych. Akurat java ma taki plus, że oferuje szeroki asortyment funkcji związanych ze Stringami. if(odczyt.charAt(0) == 'o') { String[] wartosci = odczyt.split("\t"); odleglosc = parseFloat(wartosci[1]); obrot = parseFloat(wartosci[2]); } Na początku - sprawdzamy nagłówek pakietu. Powinienem napisać warunek sprawdzający całość (equals() ), ale z racji tego że wysyłamy tylko jeden pakiet, sprawdzanie pierwszej litery wystarczy. Następnie dzielimy sobie to co przyszło na pojedyncze kawałki (tutaj się przydaje oddzielanie tabulatorem), i przypisujemy odczytane dane do zmiennych. Muszą jednak one zostać przekonwertowane do typu float, lub int (warto zapamiętać, że wartości odległości zwykle przechowuje się w float). Cały program może zatem wyglądać tak: import processing.serial.*; Serial port; float obrot = 0; float odleglosc = 200; int liczbaPolkoli = 5; void setup() { size(800, 600); port = new Serial(this, "COM1", 115200); background(0,0,0); } void draw() { pushMatrix(); translate(width/2, height-100); //srodek na srodku wykresu strokeWeight(2); noFill(); stroke(0,127,0); textAlign(CENTER); line(-width/2,0,width/2,0); float promien = (width-50)/liczbaPolkoli; for(int i = 1; i <= liczbaPolkoli; i++) { arc(0,0, promien*i, promien*i, PI, TWO_PI); // domyślnie, czyli od srodka pushMatrix(); translate(promien*i/2, 20); fill(0,127,0); text(map(promien*i,0,width,0,200), 0,0); noFill(); popMatrix(); } rotate(radians(210)); for(int i = 1; i <= 5; i++) //opisujemy półkola { line(0,0,width/2,0); pushMatrix(); translate(width/2+10, 0); rotate(radians(90)); fill(0,127,0); text(180 - (i*30) + "°", 0, 0); noFill(); popMatrix(); rotate(radians(30)); } //siatka narysowana, rysujemy linie stroke(0,255,0); pushMatrix(); rotate(PI + radians(obrot)); line(0,0,width/2,0); stroke(255,0,0); line(constrain(odleglosc*2, 0, 200),0,width/2,0); popMatrix(); popMatrix(); //wracamy do lewego gornego rogu //symulujemy zanik linii noStroke(); fill(0,4); rect(0,0,width,height); } void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt != null) println(odczyt); else return; if(odczyt.charAt(0) == 'o') { String[] wartosci = odczyt.split("\t"); odleglosc = parseFloat(wartosci[1]); obrot = parseFloat(wartosci[2]); } } void keyPressed() { port.clear(); port.write('f'); } Działanie tego urządzenia najlepiej opisze poniższy film. Bardzo przepraszam za bałagan na biurku, ale nie mogę się wziąć jakoś za sprzątanie :< No i teraz bardzo fajnie, pierwszy projekt zaliczony. Co jednak, jeżeli chcemy wysyłać dane z komputera do Arduino? Albo, co gorsza, mieć komunikację dwustronną? Jak się okazuje, nie jest to takie trudne. Zrobimy sobie kolejny projekt, tym razem trochę mniej efektowny. Przyjmujemy taki scenariusz: mamy prostego robota z czujnikiem nachylenia, nacisku, i potencjometrem do kalibracji; a za napęd stanowią 3 silniki. Aby nie komplikować sprawy i nie budować całego robota do wykonania takiego ćwiczenia, uprośćmy sprawę do 3 potencjometrów i 3 ledów: 3 potencjometry do wejść analogowych, 3 ledy do wyjść cyfrowych PWM. Myślę że każdy będzie w stanie wykonać takie ćwiczenie w praktyce. Tak wygląda wykonanie u mnie: (nie polecam potencjometrów precyzyjnych, bo trzeba się nakręcić aby zmienić wartość jakoś znacznie) Kod Arduino będzie wyglądał bardzo podobnie. Piny, zmienne, i bufor danych. #include <Arduino.h> #define PIN_CZUJNIK_WYCHYLENIA A0 #define PIN_CZUJNIK_NACISKU A1 #define PIN_POTENCJOMETR A2 #define PIN_SILNIK_A 9 #define PIN_SILNIK_B 10 #define PIN_SILNIK_C 11 int nacisk = 0; int nastawienie = 0; int wychylenie = 0; int silnikA = 0; int silnikB = 0; int silnikC = 0; char dane[64]; Funkcja setup() mówi sama za siebie, zastosowaliśmy znowu sztuczkę czekania na znak. void setup() { Serial.begin(115200); while(Serial.available() > 0) Serial.read(); while(!Serial.available()); while(Serial.available() > 0) Serial.read(); pinMode(PIN_CZUJNIK_NACISKU, INPUT); pinMode(PIN_CZUJNIK_WYCHYLENIA, INPUT); pinMode(PIN_POTENCJOMETR, INPUT); pinMode(PIN_SILNIK_A, OUTPUT); pinMode(PIN_SILNIK_B, OUTPUT); pinMode(PIN_SILNIK_C, OUTPUT); } W pętli głównej, w kwestii samych peryferiów nie trzeba za wiele robić. void loop() { nacisk = analogRead(PIN_CZUJNIK_NACISKU); wychylenie = analogRead(PIN_CZUJNIK_WYCHYLENIA); nastawienie = analogRead(PIN_POTENCJOMETR); analogWrite(PIN_SILNIK_A, silnikA); analogWrite(PIN_SILNIK_B, silnikB); analogWrite(PIN_SILNIK_C, silnikC); Napiszmy teraz standardowego ifa, sprawdzającego czy cokolwiek przyszło: if(Serial.available() > 0) { Serial.readBytesUntil('\n', dane, 64); switch(dane[0]) { case 'a': silnikA = dane[1]; break; case 'b': silnikB = dane[1]; break; case 'c': silnikC = dane[1]; break; } } Jeżeli mamy jakiekolwiek dane, wczytujemy je do bufora. Ramka danych wejściowych będzie wyglądała "xy\n", gdzie x to numer silnika, y to jego wartość. Mamy zatem 3 rodzaje pakietów. Z racji tego że operujemy tutaj na bajtach (co jest bardzo ważne), możemy zwyczajnie przypisać do zmiennej wartość z bufora, choć później dokładniej o tym powiem. Następnie może dość banalny (i niezbyt optymalny) sposób na działanie, ale jeżeli Arduino nie odebrało danych, to zawsze je może wysłać: else //jezeli nie ma danych, to wysylamy swoje dane { Serial.print("nwp"); Serial.print('\t'); Serial.print(nacisk); Serial.print('\t'); Serial.print(wychylenie); Serial.print('\t'); Serial.print(nastawienie); Serial.println('\t'); Serial.print("abc"); Serial.print('\t'); Serial.print(silnikA); Serial.print('\t'); Serial.print(silnikB); Serial.print('\t'); Serial.print(silnikC); Serial.println('\t'); } Wysyłamy 2 pakiety. W pierwszym, nacisk, wychylenie, potencjometr (przypominam, że każdy to nazywa jak chce) wysyłamy po kolei te wartości. Drugi pakiet w zasadzie nam się nie przyda, ale jest przydatny przy debugowaniu, o czym już mówię. Cały kod Arduino powinien wyglądać tak: #include <Arduino.h> #define PIN_CZUJNIK_WYCHYLENIA A0 #define PIN_CZUJNIK_NACISKU A1 #define PIN_POTENCJOMETR A2 #define PIN_SILNIK_A 9 #define PIN_SILNIK_B 10 #define PIN_SILNIK_C 11 int nacisk = 0; int nastawienie = 0; int wychylenie = 0; int silnikA = 0; int silnikB = 50; int silnikC = 255; char dane[64]; void setup() { Serial.begin(115200); while(Serial.available() > 0) Serial.read(); while(!Serial.available()); while(Serial.available() > 0) Serial.read(); pinMode(PIN_CZUJNIK_NACISKU, INPUT); pinMode(PIN_CZUJNIK_WYCHYLENIA, INPUT); pinMode(PIN_POTENCJOMETR, INPUT); pinMode(PIN_SILNIK_A, OUTPUT); pinMode(PIN_SILNIK_B, OUTPUT); pinMode(PIN_SILNIK_C, OUTPUT); } void loop() { nacisk = analogRead(PIN_CZUJNIK_NACISKU); wychylenie = analogRead(PIN_CZUJNIK_WYCHYLENIA); nastawienie = analogRead(PIN_POTENCJOMETR); analogWrite(PIN_SILNIK_A, silnikA); analogWrite(PIN_SILNIK_B, silnikB); analogWrite(PIN_SILNIK_C, silnikC); if(Serial.available() > 0) { Serial.readBytesUntil('\n', dane, 64); switch(dane[0]) { case 'a': silnikA = dane[1]; break; case 'b': silnikB = dane[1]; break; case 'c': silnikC = dane[1]; break; } } else //jezeli nie ma danych, to wysylamy swoje dane { Serial.print("nwp"); Serial.print('\t'); Serial.print(nacisk); Serial.print('\t'); Serial.print(wychylenie); Serial.print('\t'); Serial.print(nastawienie); Serial.println('\t'); Serial.print("abc"); Serial.print('\t'); Serial.print(silnikA); Serial.print('\t'); Serial.print(silnikB); Serial.print('\t'); Serial.print(silnikC); Serial.println('\t'); } } Przechodząc do processingu, nagłówek będzie wyglądał podobnie. Poza małymi tablicami bajtów. Są to nasze małe bufory, o których - i o wszystkim innym - zaraz powiem. import processing.serial.*; Serial port; int nacisk = 000; int nastawienie = 0; int wychylenie = 0; byte silnikA[] = {'a', '0', '\n'}; byte silnikB[] = {'b', '0', '\n'}; byte silnikC[] = {'c', '0', '\n'}; void setup() { size(800, 600); port = new Serial(this, "COM5", 115200); } Z racji tego że mi wystarczy jedynie obraz tego co się dzieje, to będę chciał narysować jedynie prostokąt, którego jeden bok będzie się ściskał. Wartość z potencjometru do kalibracji będzie zmieniała jego barwę, a "czujnik nachylenia", obróci go odpowiednio. Oczywiście, w prawdziwym robocie możemy stworzyć bardziej zaawansowaną wizualizację, pomagającą w debugowaniu itd. Dlatego, standardowo już, środek daję do środka okienka, odpowiednio przekształcam przed rysowaniem siatkę danych o dane odebrane z Arduino, i rysuję prostokąt. Konkretnie rzecz biorąc, jest to kształt złożony z 3 prostych i krzywej. void draw() { background(200); pushMatrix(); translate(width/2, height/2); rectMode(CENTER); stroke(0); rotate(radians(map(wychylenie, 0, 1023, -180, 180))); fill(map(nastawienie, 0, 1023, 0, 255)); beginShape(); vertex(-width/4,height/8); vertex(-width/4,-height/8); curveVertex(-width/4, -height/8 - map(nacisk, 0, 1023, 0, height)); curveVertex(-width/4, -height/8); curveVertex(width/4, -height/8); curveVertex(width/4, -height/8 - map(nacisk, 0, 1023, 0, height)); vertex(width/4, height/8); vertex(-width/4, height/8); endShape(); popMatrix(); } void keyPressed() { port.clear(); port.write('f'); } Zauważ tylko, ile razy użyliśmy width i height. Dzieląc te liczby przez odpowiednie proporcje, bardzo łatwo zrobiliśmy elastyczny i responsywny program - będzie działał w każdej rozdzielczości. Funkcję do odczytywania danych możemy przepisać praktycznie z poprzedniego przykładu. void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt == null) return; else println(odczyt); if(odczyt.charAt(0) == 'n') { String[] wartosci = odczyt.split("\t"); nacisk = parseInt(wartosci[1]); wychylenie = parseInt(wartosci[2]); nastawienie = parseInt(wartosci[3]); } I teraz tłumaczę już, dlaczego Processing i Arduino mogą się nie lubić. Przede wszystkim, Arduino posiadające zaledwie 2KB ramu bardzo nie lubi się ze Stringami, o czym można poczytać w Internecie. Dlatego (przynajmniej ja) zalecam pracę na bajtach i znakach (byte i char), ostatecznie na łańcuchach znaków i funkcji z specyfikacji języka C, a nie biblioteki String. Dlatego chcemy do Arduino przesyłać bajty, a nie ciągi znaków (String). Ale jeden znak to jeden bajt, co nam może ułatwić sprawę, nie? Otóż i tak i nie. Na pewno ułatwi nam to, że do tych zmiennych możemy przypisać zarówno 'a', jak i 48. I tutaj kryje się pułapka, bo Processing razem z javą nie mają zmiennych przyjmujących 0-255, jak byte w Arduino - zamiast tego, przyjmują wartości od -128 do 127. Arduino w takim razie, aby wartość bezpośrednio dekodować, musi zmienić tą wartość z tego zakresu na 0-255, chociażby funkcją map. Czyli Arduino nie lubi się ze Stringami, z kolei processing z bajtami... a jak zechcemy wysłać port.write("a" + silnikA + "\n"); to zgodnie z tablicą ASCII otrzymamy 3 bajty, po kolei 97, 48 (jeżeli silnik jest wyłączony), i 10, ponieważ Processing nam to połączy w Stringa. Z drugiej strony, port.write('a' + silnikA + '\n'); Działa poprawnie, ale Processing działa bardzo wolno. Dlatego, korzystając z tego że funkcja write może przyjąć typ int, byte[] lub Stringa, stworzyłem właśnie te małe bufory, które wysyłam do Arduino. Wysyłam je za każdym razem kiedy Processing odebrał dane, więc działa to na zasadzie ping-pong. Fragment programu będzie wyglądał tak: silnikA[1] = parseByte(map(nastawienie, 0, 1023, 0, 255)); silnikB[1] = parseByte(map(nacisk, 0, 1023, 0, 255)); silnikC[1] = parseByte(map(wychylenie, 0, 1023, 0, 255)); port.write(silnikA); port.write(silnikB); port.write(silnikC); oczywiście, zamiast przepisywać wartości z potencjometrów do silników powinny się tu znaleźć zaawansowane algorytmy regulatorów, dbających o poprawne działanie robota. Całość będzie wyglądała tak: import processing.serial.*; Serial port; int nacisk = 000; int nastawienie = 0; int wychylenie = 0; byte silnikA[] = {'a', '0', '\n'}; byte silnikB[] = {'b', '0', '\n'}; byte silnikC[] = {'c', '0', '\n'}; void setup() { size(800, 600); port = new Serial(this, "COM5", 115200); } void draw() { background(200); pushMatrix(); translate(width/2, height/2); rectMode(CENTER); stroke(0); rotate(radians(map(wychylenie, 0, 1023, -180, 180))); fill(map(nastawienie, 0, 1023, 0, 255)); beginShape(); vertex(-width/4,height/8); vertex(-width/4,-height/8); curveVertex(-width/4, -height/8 - map(nacisk, 0, 1023, 0, height)); curveVertex(-width/4, -height/8); curveVertex(width/4, -height/8); curveVertex(width/4, -height/8 - map(nacisk, 0, 1023, 0, height)); vertex(width/4, height/8); vertex(-width/4, height/8); endShape(); popMatrix(); } void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt == null) return; else println(odczyt); if(odczyt.charAt(0) == 'n') { String[] wartosci = odczyt.split("\t"); nacisk = parseInt(wartosci[1]); wychylenie = parseInt(wartosci[2]); nastawienie = parseInt(wartosci[3]); } silnikA[1] = parseByte(map(nastawienie, 0, 1023, 0, 255)); silnikB[1] = parseByte(map(nacisk, 0, 1023, 0, 255)); silnikC[1] = parseByte(map(wychylenie, 0, 1023, 0, 255)); port.write(silnikA); port.write(silnikB); port.write(silnikC); } void keyPressed() { port.clear(); port.write('f'); } I jak zwykle, działanie zaprezentuje najlepiej film. Teraz znowu wrócimy na chwilę do teorii. Wspominałem o tym, że Processing może wyświetlać także programy używając OpenGL. Pozwoli nam to rysować programy sprzętowo, pozwalając na turbodoładowanie, no i na wyświetlanie brył w 3D. Nie musimy pobierać żadnych bibliotek, wystarczy że w przy rozmiarze okna w size() dodamy: void setup() { size(600, 600, P3D); I od teraz nasz program będzie działał w 3D. Wiąże się to jednak z pewnymi rzeczami. Przede wszystkim, nie możemy już określać odległości od lewego górnego rogu. Nie mamy już do czynienia z płótnem, a z przestrzenią. Zatem wszystkie kształty będziemy rysować przesuwając siatkę współrzędnych. No i pozostałe proste kształty, jak linia, elipsy, prostokąty, dalej mogą zostać narysowane. Dochodzą jednak nowe kształty: box(bok); sphere(promien); kolejno pudełko i kulka. Możemy także tworzyć własne kształty za pomocą vertexów: Możemy także oteksturować nasze bryły. Jest to jednak dość trudne, do każdego vertexa dochodzą 2 argumenty: u i v, określające który kawałek obrazka ma być przyklejony na kształt. Aby załadować tekstury, ładujemy zwykły PImage i przed podaniem jakiegokolwiek vertexu po beginShape() wpisujemy texture(): Warto też zauważyć, że nie ma już rotate(), a rotateX , Y i Z, ponieważ teraz możemy obracać w 3 osiach. Kontynuując; w przypadku PShape wystarczy wywołać po prostu x.setTexture(img); Processing pozwala nawet zmienić oświetlenie sceny. lights() włączy ogólnie oświetlenie, noLights() je wyłączy. lights(); noLights(); Do dyspozycji mamy 4 rodzaje oświetlenia, choć uważam że najbardziej potrzebne będą 2 pierwsze, a 2 kolejne tylko wymienię. ambientLight(r, g, b); directionalLight(r, g, b, a, b, c); spotLight(r, g, b, x, y, z, a, b, c, r, k); pointLight(r, g, b, x, y, z); Ambient light to oświetlenie ogólne, można powiedzieć że światło dzienne. Możemy ustalić jego kolor podając r, g i b. Directional light najlepiej opisać jako Słońce; świeci się w określonym kierunku, ale daleko. A, b i c określa kierunek, przyjmuje wartości -1 - 1. Spot light można określić jako latarkę, bo ma i kolor (rgb), i kierunek(abc), i pozycję (xyz), i kąt świecenia (r), i skupienie (k). Point light to taka żarówka, więc wpisujemy jej po prostu kolor i położenie. Jeszcze jest ważna rzecz dotycząca 3D. Możemy włączyć "tryb rzutu prostokątnego": I jeżeli chodzi o 3D, tyle powinno wystarczyć do napisania dość zaawansowanej aplikacji. Oczywiście, nie omówiłem dokładnie kształtów, shaderów, oświetlenia, kamery, lecz myślę że tyle wystarczy. Spróbujmy zatem stworzyć jeszcze jeden projekt, obracającą się kostkę. Do tego przyda się Arduino z żyroskopem i akcelerometrem, np. MPU6050: I tak wygląda moja aranżacja. Nazwałem to smartHammer™. MPU jest połączone z Arduino przez I2C, i wymaga specjalnych bibliotek. #include <Arduino.h> #include "I2Cdev.h" //biblioteka I2C #include "MPU6050_6Axis_MotionApps20.h" //biblioteka MPU Następnie tworzymy mpu, zmienne pomocnicze. MPU6050 mpu; bool dmpOk = false; byte dmpStatus; //status dmp byte buforFIFO[64]; //odebrane dane z mpu Teraz zdefiniujemy dość nietypowe typy danych, które przechowają nam odczyty z czujnika. Quaternion q; // dosc smieszny typ danych VectorFloat g; // wektor trójwymiarowy, przechowujący akceleracje float ypr[3]; // tutaj będziemy trzymać kąty Po tym - już klasycznie. Myślę że kod jest klarowny: void setup() { Wire.begin(); Serial.begin(115200); Serial.println("Inicjalizacja MPU..."); mpu.initialize(); if(mpu.testConnection()) Serial.println("MPU zainicjalizowane pomyslnie."); else Serial.println("BLAD: MPU nie moglo zostac zainicjalizowane."); Serial.println("Czekam na znak, aby rozpoczac prace..."); while(Serial.available() && Serial.read()); // czyscimy bufor while(!Serial.available()); // czekamy while(Serial.available() && Serial.read()); // czyscimy bufor znowu Następnie, jeżeli wszystko działa, kalibrujemy i odpalamy DMP, moduł czujnika. W przeciwnym wypadku mówimy co poszło nie tak. if (dmpStatus == 0) { //jest dobrze mpu.CalibrateAccel(6); //kalibracja, 600 prób mpu.CalibrateGyro(6); mpu.PrintActiveOffsets(); Serial.println("Odpalam DMP..."); mpu.setDMPEnabled(true); dmpOk = true; } else { Serial.print("BLAD! Status: "); // 1 - blad pamieci Serial.print(dmpStatus); // 2 - blad dmp Serial.println("."); } } W funkcji loop() z kolei, nie wykonujemy nic jeżeli DMP nie działa, a jak mamy odczytane dane z buforu, to czytamy: obrót, akceleracje, i kąty. Kolejno yaw, pitch, roll: pochylenie, przechylenie i odchylenie: Źródło: http://calypteaviation.com/wp-content/uploads/2013/12/przechylenie-odchylenie-pochylenie.jpg Interesujące może być użycie "&". W tym wypadku nie są to operatory AND, tylko mówią kompilatorowi, żeby te zmienne nie były kopiowane. Jeżeli będę miał funkcję void która jako argument ma funkcję x, i ona zmieni wartość x, to po wykonaniu ta wartość zostanie. Tak więc tutaj funkcje te wymagają tegoż "&". Następnie wysyłay paczkę danych. Przechodząc do kodu Processingu. Nagłówek pliku będzie wyglądał, jak pozostałe, podobnie: import processing.serial.*; float x,y,z; Serial port; float YAW = 0; float PITCH = 0; float ROLL = 0; void setup() { size(600, 600, P3D); x = width/2; y = height/2; z = 0; port = new Serial(this, "COM5", 115200); } Uruchamiamy tryb 3D, oraz liczymy zmienne pomocnicze x, y, z. Użyjemy ich tutaj: void draw() { pushMatrix(); background(0); fill(255); translate(x, y, z); rotateX(radians(ROLL)); rotateY(radians(-YAW)); rotateZ(radians(PITCH)); rectMode(CENTER); box(100); Przesuwamy i obracamy. Rysujemy też pudełko. Na końcu możemy narysować tekst: popMatrix(); textSize(25); text("YAW: " + YAW, 20, height-100); text("PITCH: " + PITCH, 20, height-75); text("ROLL: " + ROLL, 20, height-50); } A funkcje odczytu przepisać z poprzednich przykładów: void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt != null) println(odczyt); else return; if(odczyt.charAt(0) == 'y') { String[] wartosci = odczyt.split("\t"); YAW = parseFloat(wartosci[1]); PITCH = parseFloat(wartosci[2]); ROLL =parseFloat( wartosci[3]); } } void keyPressed() { port.clear(); port.write('f'); } Całość będzie wyglądać tak: import processing.serial.*; float x,y,z; Serial port; float YAW = 0; float PITCH = 0; float ROLL = 0; void setup() { size(600, 600, P3D); x = width/2; y = height/2; z = 0; port = new Serial(this, "COM5", 115200); } void draw() { pushMatrix(); background(0); fill(255); translate(x, y, z); rotateX(radians(ROLL)); rotateY(radians(-YAW)); rotateZ(radians(PITCH)); rectMode(CENTER); box(100); popMatrix(); textSize(25); text("YAW: " + YAW, 20, height-100); text("PITCH: " + PITCH, 20, height-75); text("ROLL: " + ROLL, 20, height-50); } void serialEvent(Serial port) { String odczyt = port.readStringUntil('\n'); if(odczyt != null) println(odczyt); else return; if(odczyt.charAt(0) == 'y') { String[] wartosci = odczyt.split("\t"); YAW = parseFloat(wartosci[1]); PITCH = parseFloat(wartosci[2]); ROLL =parseFloat( wartosci[3]); } } void keyPressed() { port.clear(); port.write('f'); } I jak zwykle działanie pokaże filmik (jeszcze raz przepraszam za bałagan): I jeżeli chodzi o tą część, to tyle. I chyba to już nawet wszystko co planowałem wykonać w ramach kursu. Ale! Jestem świadomy że nie omówiłem ogromu możliwości Processingu. Mogę opublikować jeszcze jedną część, i tutaj pomyślałem, że może opiszę to, co chcą czytelnicy - bo opisywać wszystko co wiem i co chcę wiedzieć, to by z 10 części wyszło 😛 Jeżeli czytelnicy nie będą chcieli kolejnej części, to w takim razie gratuluję ukończenia kursu Processingu, możesz teraz tworzyć niesamowite aplikacje graficzne, łączące świat rzeczywisty z wirtualnym poprzez Arduino. GRATULACJE !- 4 odpowiedzi
-
- 2
-

-
- konkurs2021
- processing
-
(i 1 więcej)
Tagi:
-
Ten artykuł jest częścią serii "Kurs programowania w Processing" #1 - Wstęp, kształty, debugger #2 - Piksele 2D oraz interaktywność #3 - Tekst, pliki, dźwięk, przekształcenia #4 - OpenGL, Arduino! Kontynuując kurs, dzisiaj poznamy więcej rzeczy związanych z wyświetlaniem obrazu, spróbujemy odczytać i zapisać plik, oraz wytworzyć dźwięk. Postanowiłem specjalnie poświęcić chwilę czasu na przypomnienie tutaj, jak się obchodzić z klasą String. W processingu jest ona bezpośrednio zaimportowana z Javy, więc też można równie dobrze zajrzeć do jej dokumentacji. Ten artykuł bierze udział w naszym konkursie! 🔥 Na zwycięzców czekają karty podarunkowe Allegro, m.in.: 2000 zł, 1000 zł i 500 zł. Potrafisz napisać podobny poradnik? Opublikuj go na forum i zgłoś się do konkursu! Czekamy na ciekawe teksty związane z elektroniką i programowaniem. Sprawdź szczegóły » Oznacza to tyle, że wszystkie fajne funkcje z Javy są także w Processingu. Zmienną typu String możemy zatem modyfikować na tysiąc różnych sposobów – zacznijmy zatem od tych najprostszych. We wszystkich przykładach – zmienna robocza będzie nazwana „tekst”. char c = tekst.charAt(x); Zwróci znak (zmienną typu char) który jest w zmiennej tekst na pozycji x. String male = tekst.toLowerCase(); String wielkie = tekst.toUpperCase(); Te dwie funkcje zamienią wszystkie litery na małe lub wielkie. Int dlugosc = tekst.length(); Zwróci liczbę znaków zawartą w zmiennej tekst. Jeżeli ktoś nie pracował nigdy ze stringami, to powinien zapamiętać jak się je porównuje: String a = "korona"; Strinb b = "korona"; if(a.equals(b)) zrobCos(); //jezeli b jest rowne a W teorii można by użyć „==”, lecz może to wprowadzić trudne potem do wykrycia błędy. Stringi można także łączyć operatorem „+”: String hellothere = "hello" + "there"; String wiadomosc = "Liczba zakażonych: " + x + " tysięcy"; Do tworzenia filtrów może się także przydać replace: a = a.replace("do zmienienia", "zmiana"); Aby znaleźć w tekście dany ciąg znaków, posłuży do tego funkcja: int x = tekst.indexOf("tekst do wyszukania"); Jedną z ciekawszych funkcji jest substring(). Pozwala ona wydzielić ze Stringa kawałek tekstu: String tekscik = tekst.substring(6, 11); Aby podzielić tekst, np. długie zdanie na pojedyncze wyrazy (oddzielone spacjami), bardzo przydatna będzie tutaj funkcja split(). String[] wyrazy = split(tekst, " "); Przede wszystkim - funkcja ta zwraca tablicę Stringów, a nie jeden String. Do wypisania całej tablicy użyłem funkcji printArray, która wypisuje w konsoli wszystkie elementy tablicy. Do dyspozycji mamy jeszcze funkcję join(), która działa dokładnie na odwrót: skleja nam tablicę stringów w jeden, i oddziela je separatorem. String zdanie = join(wyrazy, " "); Po przypomnieniu sobie obchodzenia się ze Stringami, dokończmy rozdział o kształtach. W poprzednich częściach, wszystko rysowaliśmy za pomocą najprostszych kształtów. Niedawno nauczyliśmy się rysować złożone krzywe – czas sobie tą wiedzę uporządkować. Także Processing daje nam możliwość tworzenia poligonów, wielokątów. Rysowanie ich jest trochę bardziej złożone: beginShape(); vertex(x1, y1); vertex(x2, y2); //itd. endShape(); Tak naprawdę wszystkie kształty, i nasze, i te najprostsze, to są obiekty PShape. Dzięki bezpośredniemu dostępowi do PShape, możemy rysować bardziej optymalnie niż kształt po kształcie. Nie przedłużając: PShape prostokat = createShape(RECT, 100, 100, 100, 50); No, udało nam się inaczej zrobić prostokąt. Aby teraz go narysować, w funkcji draw() wystarczy wpisać shape(prostokat); co da nam poniższy efekt: Jedną z zalet takiego rysowania kształtów jest taka, że możemy tylko do danego kształtu przypisać właściwości rysowania: Jeżeli chcemy rysować własne kształty, także możemy to zrobić, i to wykorzystując stare funkcje – wystarczy się odwołać do danego PShape. Przydatna dla niektórych może być także funkcja wczytująca kształt z pliku .svg: prostokat = loadShape(„plik.svg”); Przechodząc teraz do plików: jeżeli chcemy odczytywać dane z różnych plików – czy to danych do wykresu, czy zmiennych do robota – najprościej byłoby je zapisywać w oddzielnym pliku, niż za każdym razem zmieniać program. Zaczniemy od najzwyczajniejszych plików .txt – przykładowy plik: koronaferie reaktywacja marzec 2021 W Processingu plik tekstowy ładujemy podobnie jak obrazy, czyli Processing będzie szukał danego pliku w swoim katalogu szkicu – jeżeli nie wiesz jak się tam dostać, zostało to opisane w poprzedniej części. Plik tekstowy ładujemy do tablicy Stringów – każdy wiersz to jeden String. String[] dokument = loadStrings("plik.txt"); println("Ten plik ma " + dokument.length + " wierszy."); Wczytany tekst możemy dowolnie obrabiać. Możemy także zapisać plik, wystarczy wywołać saveStrings(): saveStrings("dane.txt", tablicaStringow); Teraz na chwilę wrócimy do poprzedniej części, by wykorzystać tą wiedzę w praktyce. Do napisania był program liczący reaktancje w układzie RLC – mój wyglądał tak: float pojemnosc = 0.00001; //w faradach float indukcyjnosc = 0.01; //w henrach float czestotliwosc = 2000; //w hercach float rezystancja = 100; //w omach int offset = 100; void setup() { size(800,400); //inicjalizacja background(255); stroke(0); fill(0); textSize(20); line(0, height/2, width, height/2); //uklad wspolrzednych line(offset, 0, offset, height); triangle(offset, 0, offset + 2, 15, offset - 2, 15); triangle(width, height/2, width - 15, height/2 - 2, width - 15, height/2 + 2); text("f [Hz]", width - textWidth("f [Hz]") - 4, height/2 + 25); text("X, R [Ω]", 92 - textWidth("X, R [Ω]"), 25); fill(255,0,0); textSize(12); text("czerwony - reaktancja", width-200, height-100); fill(0, 255, 0); text("zielony - kapacytancja", width-200, height-80); fill(255, 0, 255); text("fioletowy - rezystancja", width-200, height-60); fill(0, 0, 255); text("niebieski - moduł impedancji", width-200, height-40); float fr = 1 / (TWO_PI * sqrt(pojemnosc * indukcyjnosc)); fill(0); text("częstotliwość rezonansowa = " + fr + "Hz", width-300, 250); for(int i = 1; i <= czestotliwosc; i++) { float Xl = TWO_PI * i * indukcyjnosc; //liczymy float Xc = 1 / (TWO_PI * i * pojemnosc); float X = Xl - Xc; float Z = sqrt(pow(rezystancja, 2) + pow(X, 2)); strokeWeight(2); stroke(255, 0, 0); point(map(i, 0, czestotliwosc, offset, width), map(Xl, height/2, -height/2, 0, height)); stroke(0, 255, 0); point(map(i, 0, czestotliwosc, offset, width), map(Xc, height/2, -height/2, 0, height)); stroke(255, 0, 255); point(map(i, 0, czestotliwosc, offset, width), map(rezystancja, height/2, -height/2, 0, height)); stroke(0, 0, 255); point(map(i, 0, czestotliwosc, offset, width), map(Z, height/2, -height/2, 0, height)); } } Na początku definiujemy stałe, dla jakich elementów liczymy wartości. W funkcji setup są standardowe funkcje, jak przygotowanie tła, kreski itd. - następnie jest rysowany układ współrzędnych i niektóre stałe. Pętla for maluje kropka po kropce wykresy, zgodnie z ich wzorami. Mógłbym oczywiście zrobić tutaj kształt wykorzystując vertexy, lecz myślę że taki program wystarczy na potrzeby przykładu. Jak widać, jest tam dużo funkcji map() wykorzystujących width i height – pomagają one zachować responsywność aplikacji przy innych rozdzielczościach niż domyślna: Użyłem jednak kilku stałych, takich jak offset, w teorii powinny być one wyliczane na podstawie szerokości/wysokości Teraz, jeżeli chcielibyśmy zmienić elementy na inne, musielibyśmy zmieniać za każdym razem kod programu. Spróbujmy zaimplementować zatem obsługę plików – przede wszystkim zmieniając domyślne wartości na 0 float pojemnosc = 0; //w faradach float indukcyjnosc = 0; //w henrach float czestotliwosc = 0; //w hercach float rezystancja = 0; //w omach a następnie stworzyć ową tablicę Stringów: String[] plik = loadStrings("plik.txt"); i przypisać wartości z tablicy: pojemnosc = parseFloat(plik[0]); //w faradach indukcyjnosc = parseFloat(plik[1]); //w henrach czestotliwosc = parseFloat(plik[2]); //w hercach rezystancja = parseFloat(plik[3]); //w omach Tak więc nagłówek kodu będzie u mnie wyglądał tak: float pojemnosc = 0; //w faradach float indukcyjnosc = 0; //w henrach float czestotliwosc = 0; //w hercach float rezystancja = 0; //w omach int offset = 100; void setup() { size(800,400); //inicjalizacja background(255); stroke(0); fill(0); textSize(20); String[] plik = loadStrings("plik.txt"); pojemnosc = parseFloat(plik[0]); //w faradach indukcyjnosc = parseFloat(plik[1]); //w henrach czestotliwosc = parseFloat(plik[2]); //w hercach rezystancja = parseFloat(plik[3]); //w omach // reszta kodu taki kod wyeksportowałem (Plik > Wyeksportuj aplikację), po zmienieniu wartości w pliku – pozostaje cieszyć się efektem. Widać też że jednak powinno się rysować wykresy funkcji korzystając z kształtów, nie kropek... Po udanej obsłudze plików tekstowych, przenieśmy się spowrotem do czcionek. Processing obsługuje czcionki wbudowane (domyślną), systemowe (zainstalowane na komputerze), oraz wczytane. Listę czcionek systemowych możemy elegancko odczytać tym kodem: String[] fontList = PFont.list(); printArray(fontList); Dość podobnie jak odczytując z pliku, każda linijka to każda nazwa czcionki. Odwołujemy się tutaj do PFont, obiektu czcionki. Znowu korzystamy z printArray aby wszystko wypisać Aby użyć czcionki systemowej, musimy ją najpierw „przekonwertować” w format zrozumiały dla processingu. Tworzymy zatem nową zmienną: Pfont czcionka; Następnie przypisujemy do niej wybraną czcionkę. czcionka = createFont(„Txt”, 32); Funkcja createFont może przyjąć trzy wartości: źródło czcionki, jej wielkość, i antyaliasing (true albo false). Po zapisaniu tej funkcji zostało teraz pisać tą czcionką: textFont(czcionka); text(„koronaferie: reaktywacja”, 0, 100); Całość powinna wyglądać tak: Wczytywanie czcionki z pliku jest równie proste. Do folderu ze szkicem dołączamy czcionkę, i zamiast samej nazwy w createFont, dodajemy format. Idąc dalej, bardzo ciekawą funkcją processingu są przekształcenia samej siatki współrzędnych. Daje to ogrom możliwości, a przede wszystkim może ułatwić rysowanie wykresów, bo środek płótna możemy ustawić na środek okienka. Przede wszystkim trzeba zapamiętać, że każdy narysowany element po przekształceniu nie zmieni swojego położenia; tylko siatka współrzędnych się przestawi. Mogą się pojawić pytania „po co przestawiać siatkę, skoro możemy narysować element w innym miejscu?” - spróbuję pokazać, że przestawianie siatki może okazać się bardziej optymalne. Zacznijmy zatem od narysowania dwóch punktów, jeden o współrzędnych (10,10) a drugi na (30,30). Spróbujmy teraz narysować ten sam punkt, ale uzyskać przy okazji ten sam efekt – czyli przesunąć go o wektor. Punkt czerwony został przesunięty o wektor [20,20], więc znalazł się na koordynatach (30,30). Spróbujmy zatem nie „przesuwać” punktu, a całą siatkę. Jak widać, dzięki translate() udało nam się przesunąć całą siatkę o wektor [20,20]. Dzięki temu punkt (10,10) narysowaliśmy dwa razy, a jednak w różnych miejscach. Spróbujmy to samo, ale z drugim przykładem: krzywą Beziera. Jak widać, każdy punkt tutaj musimy ręcznie „przesunąć”. Przy bardziej złożonych kształtach, po prostu bardzo się napracujemy. O wiele prościej można przesunąć siatkę: To teraz sprawdźmy co się stanie, jak przesuniemy siatkę trzeci raz. Jak widać, siatkę przesuwamy relatywnie, czyli dodajemy i odejmujemy od aktualnej wartości położenia siatki. Po wielu przesunięciach, możemy nawet nie wiedzieć jak wrócić do lewego górnego rogu! Dlatego bardzo często stosuje się komendy push i popMatrix. Jak widać, ostatnia niebieska krzywa nałożyła nam się na pierwszą, czerwoną. PushMatrix zapisuje obecną pozycję siatki „do schowka” - u nas przed jakimkolwiek przekształceniem – a po przekształceniach wracamy do lewego górnego rogu, przez popMatrix. Oczywiście, moglibyśmy siatkę przesunąć o wektor [-40, -40], lecz w bardziej zaawansowanych programach, prawdopodobnie nie będziemy wiedzieli o jaki wektor przesunąć siatkę, by wrócić dokładnie w lewy górny róg. Co więcej, siatkę poza przesuwaniem, możemy obracać! Jednak przypomnę jeszcze raz, że w Processingu kąty podajemy w radianach. Na szczęście Processing ma wbudowaną funkcję radians(x), która zwróci wartość radianów z podanego kąta w stopniach. 0 radianów (0 stopni) znajduje się maksymalnie po prawej stronie, czyli na wschód. Południe to będzie pi/2, zachód pi, a północ, czyli 270 stopni, to 3pi/2 radianów. Funkcją odpowiedzialną za obrót jest rotate() - spróbujmy krzywą obrócić o 45 stopni: Aby efekt był bardziej widoczny, środek całości dałem na środek okienka. Czerwona krzywa jest zatem „oryginalną”, a zielona jest obrócona o 45 stopni. Jeszcze raz, popMatrix przywróci wszystko do lewego górnego rogu. Żeby pokazać dokładnie jak działa obrót, spróbujmy taki przykład: Myślę, że teraz kwestia obrotu stała się klarowna. Pamiętaj, że jeżeli obrócimy siatkę zbyt bardzo, obraz może być poza obszarem okienka i się nie wyświetlić! Przede wszystkim – siatka obraca się względem swojego punktu (0, 0). Dlatego ustawiłem go na środek okienka, żeby zrobić takie ładne „koło”. Ostatnią funkcją operacji na siatce jest scale(). Pozwala przeskalować obraz względem punktu (0, 0): Wyraźnie widać, że praktycznie wszystkie wartości są narysowane tutaj dwa razy więcej. I kreska jest 2x grubsza, kwadrat dwukrotnie większy, i dwa razy dalej jest oddalony od lewego górnego rogu. A jednak jest to ten sam kwadrat, tylko powiększony dwa razy. Scale() przyjmuje liczbę typu float, więc możemy siatkę zmieniać o ułamki. Spróbuj samemu! Warto jeszcze zaznaczyć, że bardziej uważni czytelnicy mogą natrafić na taki problem: Jeżeli funkcja draw() wykonuje się 60 razy na sekundę, i tyle samo razy przekształcam siatkę, to po chwili powinna być ona zupełnie inna, tutaj: kwadrat powinien się stawać coraz większy (siatkę powiększam dwukrotnie, potem znowu, i znowu). Na szczęście siatka samoczynnie wraca do lewego górnego rogu za każdym razem, kiedy funkcja draw() jest wywoływana – więc nie ma się czym martwić. Jak do tej pory, Processing umożliwiał nam zabawę tylko obrazem. Do Processingu, zarówno jak i do Arduino, istnieje mnóstwo przeróżnych bibliotek – dzięki czemu Processing może połączyć się z dowolnym API, odczytać temperaturę procesora komputera itd. Dzisiaj wgramy pierwszą bibliotekę, umożliwiającą nam pracę z dźwiękiem. Musimy zacząć od wgrania biblioteki – na szczęście Processing ma wbudowany menedżer bibliotek. Wchodzimy w Szkic > Importuj bibliotekę > Dodaj bibliotekę. Pokazuje nam się nowe okienko: Jak widać, naprawdę jest wiele bibliotek do zainstalowania. I to tylko domyślnych! Wyszukujemy bibliotekę „sound”, konkretnie tą od Processing Foundation: Instalujemy, i jak dostaniemy taką informację: Możemy zamknąć okienko menedżera. Następnie importujemy bibliotekę: Jak widać, wpisała nam się następująca linijka: import processing.sound.*; zamiast #include, mamy import*, zapożyczone z javy: dołączamy do programu wszystko zawarte w paczce processing.sound. Spróbujemy teraz wygenerować dźwięk – proces ten jest zwany syntezą; pierwsze elektroniczne syntezatory powstały w latach 60. ubiegłego wieku, umożliwiając rozkwit całkowicie nowej muzyki – zaczynając od prawdopodobnie nieznanych już „popcorn”, czy „I feel love”. Wszystkie dźwięki w tych utworach są wygenerowane przez elektronikę. Oczywiście, dźwięk w tych utworach to coś więcej niż zwykła sinusoida, czy kwadrat; można powiedzieć, że to różne dźwięki się nakładają. Spróbujmy zatem stworzyć syntezator składający się z 4 podstawowych dźwięków, a będą to sinusoidy o różnych częstotliwościach. Dlatego stwórzmy tablicę sinusów, ich liczbę, oraz tablicę ich częstotliwości: SinOsc[] sinusy; float[] czestotliwosc = {200, 440, 500, 1000}; int liczbaGeneratorow = 4; Następnie, podobnie jak każdy inny element, definiujemy nasze tablice. Sinusy = new SinOsc[liczbaGeneratorow]; Pojawiło się słówko kluczowe new; oznacza ono, że do danej zmiennej przypisujemy już dane miejsce w pamięci. W przeciwnym wypadku, może nas dopaść java: Tak więc stworzyliśmy generatory – teraz musimy je skonfigurować, najlepiej będzie to zrobić w pętli for(): for(int i = 0; i < liczbaGeneratorow; i++) { } I teraz musimy przemyśleć, jak chcemy skonfigurować nasze oscylatory. Przede wszystkim każdy z nich musi mieć inną głośność (amplitudę), i inną częstotliwość. Zacznijmy od obliczenia amplitudy dla każdego z nich: float amp = (1.0 / liczbaGeneratorow) / (i+1); To jest przykładowy sposób, możemy także sztywno ustawić, że pierwszy ma mieć głośność 0.1, drugi 0.35, itd. - wartości powinny być od 0 do 1. Częstotliwości na razie zostawię z góry ustalone. Kontynuując, musimy już konkretnie stworzyć nasze oscylatory. sinusy[i] = new SinOsc(this); Tym razem jest słowo „this”. Wskazuje ono na obiekt, dla którego został on wywołany. Można powiedzieć, że po prostu tworzymy już fizycznie nasze syntezatory. Jak widać java nie jest łatwa. Bez zrobienia tego kroku dostaniemy 𝕟𝕦𝕝𝕝 𝕡𝕠𝕚𝕟𝕥𝕖𝕣 𝕖𝕩𝕔𝕖𝕡𝕥𝕚𝕠𝕟. Teraz zostało już ustawić częstotliwość generatorów: sinusy[i].freq(czestotliwosc[i]); oraz głośność: sinusy[i].amp(amp); Na końcu zostało generatory włączyć. sinusy[i].play(); Proponuję tylko przed uruchomieniem programu wyciszyć system, aby przez przypadek nie być niemile uderzonym falą czystej sinusoidy. Całość powinna wyglądać tak: import processing.sound.*; SinOsc[] sinusy; float[] czestotliwosc = {200, 440, 500, 1000}; int liczbaGeneratorow = 4; void setup() { size(200, 200); background(255); sinusy = new SinOsc[liczbaGeneratorow]; for (int i = 0; i < liczbaGeneratorow; i++) { float amp = (1.0 / liczbaGeneratorow) / (i+1); sinusy[i] = new SinOsc(this); sinusy[i].freq(czestotliwosc[i]); sinusy[i].amp(amp); sinusy[i].play(); } } void draw() { } Po odtworzeniu programu, powinniśmy zostać przywitani dźwiękiem. Jest on połączeniem wszystkich 4 oscylatorów. Aby zrobić program ciekawszym, możemy zmodyfikować program aby zmieniał częstotliwość względem położenia myszki: void draw() { float f = map(mouseY, 0, height, 20, 10000); for(int i = 0; i < liczbaGeneratorow; i++) sinusy[i].freq(f); } Po odtworzeniu programu, możemy teraz sterować częstotliwością. Problem w tym, że każdy oscylator teraz gra tak samo. Spróbujmy zatem wprowadzić jakąś "niedoskonałość": void draw() { float f = map(mouseY, 0, height, 20, 10000); float d = map(mouseX, 0, width, -1, 1); for(int i = 0; i < liczbaGeneratorow; i++) sinusy[i].freq(f * (i + 1 * d)); } Teraz pozycja kursora w osi X spowoduje zmianę częstotliwości każdego oscylatora. Poza oscylatorem sinusoidy, mamy do wyboru WhiteNoise(); //szumy, pewnie chodzi o barwę dźwięku PinkNoise(); BrownNoise(); SinOsc(); //sinusoida SawOsc(); //piła SqrOsc(); //kwadrat TriOsc(); //trójkąt Pulse(); //pwm Jeżeli jednak zależy nam nie na syntezie dźwięku, a na jego odtwarzaniu – wystarczy zamiast oscylatora zdefiniować plik dźwiękowy: SoundFile[] plik; Wczytać plik: plik = new SoundFile(this, „sciezkadopliku.mp3”); I go włączyć. plik.play(); Więc całość może wyglądać tak: Problem może być tylko taki, że dźwięk zostanie odtworzony dopiero po załadowaniu w całości. I jeżeli chodzi o dźwięk, to biblioteka ta daje o wiele więcej możliwości, więc jeżeli ktoś chce je zgłębić – zapraszam do dokumentacji. W następnej części w końcu połączymy Processing z Arduino, spróbujemy zrozumieć wyświetlanie przy użyciu OpenGL, i omówimy niektóre, przykładowe programy oraz algorytmy. Proponuję już nie wykonać żadnego programu specjalnie, a po prostu pobawić się możliwościami, przede wszystkim zrozumieć, jak to wszystko działa.
-
Ten artykuł jest częścią serii "Kurs programowania w Processing" #1 - Wstęp, kształty, debugger #2 - Piksele 2D oraz interaktywność #3 - Tekst, pliki, dźwięk, przekształcenia #4 - OpenGL, Arduino! W kolejnej części kursu, opowiemy sobie o funkcjach i mechanizmach rysowania w Processingu, kilku wbudowanych funkcjach, i spróbujemy zrobić prosty kalkulator. Zaczynajmy! Ten artykuł bierze udział w naszym konkursie! 🔥 Na zwycięzców czekają karty podarunkowe Allegro, m.in.: 2000 zł, 1000 zł i 500 zł. Potrafisz napisać podobny poradnik? Opublikuj go na forum i zgłoś się do konkursu! Czekamy na ciekawe teksty związane z elektroniką i programowaniem. Sprawdź szczegóły » Rysowanie W poprzedniej części przyswoiliśmy kilka prostych funkcji, pozwalających rysować podstawowe kształty. Jeżeli dla kogoś nie było klarowne jak to „działa”, to teraz omówimy mechanizm rysowania. Przede wszystkim, należy sobie wyobrazić okienko naszego programu jako płótno, po którym można malować. I żeby było łatwiej, wyobraźmy sobie że za nas rysuje robot, który wykonuje nasze polecenia. Zaczynając od pierwszego programu z poprzedniej części: size(200, 200); background(255); stroke(0); circle(100,100,40); Najpierw mówimy robotowi, że nasze płótno ma mieć rozmiar 200x200 pikseli (odpowiednio szerokość, i wysokość), oraz białe tło. Następnie robot bierze do ręki czarny pędzel (stroke), i wie, że ma nim malować kontury kształtów. Aby narysować okrąg, mówimy robotowi teraz żeby po prostu narysował go – o średnicy 40 pikseli, ze środkiem odległym o 100 pikseli w x i 100 pikseli w y od lewego górnego rogu. Można powiedzieć, że nasze płótno to układ współrzędnych, ze środkiem w lewym górnym rogu. Jeżeli chcemy mieć czerwone koło z białym konturem na czarnym tle, program powinien wyglądać tak: size(200, 200); background(0); stroke(255); fill(255,0,0); circle(100,100,40); Dla niektórych może nie być jasne, dlaczego polecenie "wypełnij", jest przed "pomaluj koło". Jeszcze raz: robot bierze tym razem biały pędzel, czerwone wiaderko farby, i dopiero tymi narzędziami rysuje koło. Warto zapamiętać taką zasadę, że najpierw mówimy jak takie koło ma wyglądać, a dopiero potem je malujemy. Pozwoli to uniknąć błędów! Uzupełniając jeszcze zbiór kształtów: możemy narysować trójkąt. triangle(x1, y1, x2, y2, x3, y3); x1, y1 - współrzędne pierwszego wierzchołka, x2, y2 - drugiego, i x3 oraz y3, to współrzędne trzeciego wierzchołka. Grubość kreski zaś możemy zmienić funkcją strokeWeight(x); po zbiór wszystkich funkcji jakie mamy do dyspozycji, warto zajrzeć do oficjalnej dokumentacji. noStroke() usunie kontur w ogóle. Kolory Polecenia przyjmujące kolor (np. fill, stroke, background) mogą przyjmować albo jedną zmienną, albo trzy, a czasem nawet cztery lub dwa. Zmienne te są pojedynczymi bajtami ośmiobitowymi (typu byte, char), więc przyjmują wartości od 0 do 255 – gdzie zero oznacza minimalną wartość, 255 maksymalną wartość. Dla przypomnienia, konkretnie byte/char ma 8 bitów, więc obraz czarnobiały będzie z głębią ośmiobitową, gdzie kolorowy – już 24 bity. Zmienne typu int mogą mieć wartości większe od zakresu char/byte, więc aby ją wykorzystać, trzeba ją zmodyfikować - o czym za chwilę. Wracając do samych funkcji; możemy podać tylko jedną wartość, wtedy obraz będzie narysowany w skali szarości. Przy podaniu dwóch wartości, pierwsza będzie kolorem w skali szarości, a druga alfą - przezroczystością. Możemy także podać 3 wartości; komponent czerwony, zielony i niebieski, które po wymieszaniu mogą nam dać praktycznie dowolny kolor. Może się tutaj przydać wbudowany w Processing wybierak barw: Czasem przydatne może być podanie czwartej wartości, alfy. Jest to przezroczystość – gdzie 0 oznacza że kształt jest całkowicie przezroczysty, a 255 – całkowicie nieprzezroczysty. fill(127); //50% jasności fill(255, 127); //biały półprzezroczysty fill(255, 0, 255); //fioletowy fill(255, 0, 0, 127); //czerwony półprzezroczysty W wybieraku są jednak jeszcze 3 wartości: H, S i B. Oznaczają one kolejno hue (odcień), saturation (nasycenie), oraz brightness (jasność, czasem value). Tymi trzema wartościami także można definiować kolory, zamiast R, G i B. Źródło: https://nycdoe-cs4all.github.io/images/lessons/unit_1/3.2/pie.png Wizualnie możemy to przedstawić jako taki walec. Dla niektórych taka postać może być bardziej naturalna, więc może kolor podawać także w tych wartościach: colorMode(HSB); Wtedy należy będzie podawać kolejno wartości HSB w przedziale 0-255. Jeżeli jednak chcemy jeszcze "naturalniej" podawać kolory, możemy podać zakres wartości: colorMode(HSB, 360, 100, 100); //podaliśmy kolejno hue, saturation i brightness Dzięki tej funkcji, kolor możemy definiować zgodnie z naszym walcem: jako że koło ma 360 stopni, możemy wybrać kolor tak jak jest na walcu, a nasycenie i jasność podać w procentach, od 0 do 100. Przydatnym trikiem może być funkcja constrain(a, min, max); która ograniczy liczbę a do podanych wartości (dlatego np. nie będzie miała więcej niż 255). Inną przydatną funkcją może być map(a, min1, max1, min2, max2); Która przekonwertuje wartość a z jednej skali do drugiej (np. wartość 100 ze skali 0-200 do 500 w skali 0-1000, czyli 50%). Przede wszystkim, kolor należy brać jako rodzaj zmiennej. Dlatego możemy zrobić coś takiego: color x = #ff0000; color y = color(255, 0, 0, 0); Możemy tym sposobem przypisywać wartości kolorów, albo robić zmienne zawierające z góry ustalone kolory. Tekst Poza prostymi kształtami, dobrze by było umieć narysować tekst. Processing pozwala korzystać z wbudowanej czcionki, oraz własnej; na razie będziemy korzystać z domyślnej. text(tekst, x, y); Narysuje zmienną "tekst", która może być zarówno liczbą, jak i Stringiem. "x" jest liczony od lewej krawędzi tekstu, a co ważne, y jest liczony od dolnej krawędzi tekstu. Co jeszcze ważniejsze, kolor nie definiujemy przez "stroke", a "fill" ! Tekst możemy narysować także w prostokącie. Jeżeli tekst będzie za długi, zostanie ucięty. Pierwszy parametr to zmienna do wyświetlenia, dwa następne to odpowiednio x i y lewego górnego rogu prostokąta, a dwa następne to szerokość i wysokość prostokąta. text(tekst, x1, y1, szerokosc, wysokosc); Rozmiar tekstu definiujemy przez podanie wysokości w pikselach: textSize(a); Odstęp pomiędzy liniami tekstu możemy zmienić tą funkcją: textLeading(a); Możemy także zmienić miejsce od którego będzie rysowany tekst - od lewej krawędzi, środka, i prawej krawędzi. textAlign(LEFT); textAlign(CENTER); textAlign(RIGHT); Bardzo przydatna może się jeszcze przydać funkcja zwracająca długość tekstu przed jego wyświetleniem. int dlugosc = textWidth(zmienna); Krzywe Bardzo często będziemy wykorzystywać krzywe w celu narysowania wykresu, konkretnego kształtu itp. W Processingu możemy narysować 3 rodzaje krzywych. Zaczynając od zwykłego łuku - łuk jest wycinkiem elipsy. Dlatego będziemy go rysować podobnie jak elipsę; pierwsze 4 zmienne są zatem takie same, jakbyśmy rysowali elipsę (kolejno współrzędne lewego górnego rogu prostokąta, szerokość i wysokość). Dochodzą jeszcze 2 parametry, kąt startowy i końcowy. arc(x1, y1, szerokosc, wysokosc, start, stop); Należy pamiętać, że w Processingu kąty są podawane w radianach (pi radianów = 180 stopni), a zero stopni jest z prawej strony prostokąta. Pozostałe krzywe dla bardziej zaawansowanych użytkowników, szczególnie tych, którzy dobrze znają trygonometrię. Krzywą możemy narysować funkcją curve(): curve(punktp1x, punktp1y, punkt1x, punkt1y, punkt2x, punkt2y, punktp2x, punktp2y); Dość szeroka ta funkcja. Do zdefiniowania krzywej potrzebujemy 4 punktów: startowego i końcowego krzywej (punkt1x i y, punkt2x i y), oraz dwóch pomocniczych (punktp1x i y, punktp2x i y). Jak pomocnicze punkty oddziałują na tą krzywą? Tutaj najlepiej samemu się tym pobawić, ponieważ definicja jest trochę długa i mało zrozumiała dla przeciętnej osoby. Najprościej jednak będzie dla nas rysować krzywe Beziera. Trochę łatwiej jest zrozumieć jak one działają: bezier(punkt1x, punkt1y, punktp1x, punktp1y, punktp2x, punktp2y, punkt2x, punkt2y); Cóż, funkcja ta także przyjmuje 4 punkty, jeden startowy i końcowy, oraz 2 pomocnicze. Warto zauważyć, że ich kolejność jest inna. Działanie punktów kontrolnych tutaj jest trochę prostsze: można sobie wyobrazić, że te punkty są połączone z krzywą gumką recepturką. Im dalej pociągniemy tym bardziej wykrzywimy naszą linię. Jeżeli chcemy zdefiniować więcej punktów aby zrobić bardziej wyrafinowaną krzywą, musimy to zrobić w trochę niestandardowy sposób: beginShape(); vertex(x, y); //pierwszy punkt bezierVertex(punktp1x, punktp1y, punktp2x, punktp2y, punktx, punkty) endShape(); Aby zrobić taką długą krzywą, musimy zrobić nowy kształt. BeginShape() powie naszemu robotowi z początku artykułu, że chcemy zrobić "coś większego". Następnie definiujemy pierwszy punkt – vertex – a zaraz po nim kolejne punkty Beziera, ile ich chcemy. Na koniec mówimy robotowi że kształt został narysowany, i że kończymy jego rysowanie funkcją endShape(). W ten sposób możemy też rysować wieloboki, podając zwykłe vertexy - o czym dokładniej w kolejnej części. Należy zwrócić uwagę na wygląd krzywych cure i bezier, a mają takie same punkty początkowe i pomocnicze! (dokonałem tylko przesunięcia w osi y o 100) Krzywymi Beziera można się też pobawić w programie GIMP: Zdjęcia i obróbka pikseli Processing umożliwia także wczytywanie i obróbkę zdjęć, a nawet ich zapis. Przechodząc od razu do kodu: PImage img; //zmienna typu PImage void setup() { size(500, 500); img = loadImage("mysummervacation.jpg"); //robimy nowy obiekt typu PImage, ładując plik do zmiennej } void draw() { background(0); image(img,0,0); //rysujemy obrazek na koordynatach 0,0 } Tym kodem wczytamy i wyświetlimy zdjęcie z pliku. Tworzymy najpierw zmienną typu Pimage, a następnie deklarujemy obiekt przypisując zdjęcie do tej zmiennej. Na końcu zdjęcie wyświetlamy. Troszkę jest to na odwrót zrobione, lecz powinno być to zrozumiałe. Processing wczyta plik który znajduje się w głównym katalogu szkicu - możemy się tam dostać z poziomu menu, lub klikając CTRL+K: Skoro mamy już zdjęcie, to możemy teraz coś z nim zrobić. Na początek wystarczy nam zmiana odcienia: tint(kolor); Gdzie za kolor należy wstawić wartości rgb lub skalę szarości. Mówiąc o zdjęciu jako pliku, powinniśmy raczej myśleć że jest to zbiór pikseli (w grafice rastrowej). Każdy piksel ma swoją wartość i swój numer – piksel zerowy jest w lewym górnym rogu, i co ważne, zdjęcie nie jest tablicą dwuwymiarową, tylko jednowymiarową – czyli każdy piksel ma po prostu swój numer. Jeżeli mamy zdjęcie 5x5 pikseli, pierwszy piksel będzie o numerze 0, ostatni 24, co da nam 25 pikseli. Pierwszy wiersz będzie miał zatem piksele 0-4, a ostatni – 20-24. Przydatny może się okazać wzór: px = x + (y*szerokosc) Który nam określi numer danego piksela z współrzędnych x i y. Tak więc piksel o współrzędnych (4,3) to 4 + 3 * 5 = 19. W processingu mamy bezpośredni dostęp do naszego płótna, czyli zbioru pikseli – lecz przed edytowaniem go, musimy go "załadować": loadPixels(); pixels[i] = color(x); pixels[] to nasze płótno. Możemy traktować je jako zwykłą zmienną typu color. Po zmianie tej wartości, musimy "zaktualizować" płótno aby zobaczyć nowe piksele: updatePixels(); Co więcej, funkcje te możemy wywołać w stosunku do zdjęcia: img.loadPixels(); Możemy dzięki temu stworzyć nasze własne filtry do zdjęć - na przykład wyświetlmy obraz o dwukrotnie większej saturacji, lub wyświetlimy tylko czerwone piksele. Przydatne będą tu funkcje red(), blue() i green() które wyciągną z koloru konkretną wartość. Klawiatura i mysz W poprzedniej części poznaliśmy dwie zmienne programu, mouseX i mouseY, wskazujące koordynaty kursora. W stosunku do myszki mamy jeszcze do dyspozycji zmienną mousePressed(), która zwraca LEFT, CENTER oraz RIGHT, w zależności od wciśniętego przycisku. Oczywiście Processing obsługuje też klawiaturę. Zmienna keyPressed() zwraca logiczne 1, kiedy jest przyciśnięty przycisk. Z kolei zmienna key zwróci wciśnięty znak. Jeżeli chcemy odczytać klawisz funkcyjny, jak alt, ctrl czy delete, przychodzi nam tutaj zmienna keyCode, która może zwrócić: -ALT -CONTROL (CTRL) -SHIFT -UP (strzałka w górę) -DOWN (strzałka w dół) -LEFT (strzałka w lewo) -RIGHT (strzałka w prawo) Pozostałe klawisze jak enter, backspace, esc itd możemy odczytać przez key, ponieważ są one w specyfikacji ASCII. Przydatne mogą być także "eventy", czyli funkcje wywoływane kiedy coś się stanie (przerwania): mousePressed() wywoła się raz, kiedy myszka jest naciśnięta mouseReleased() wywoła się raz, kiedy odklika się myszkę mouseMoved() wywoła się raz, kiedy myszka się przesunie mouseDragged() wywoła się raz, kiedy myszka będzie kliknięta i się przesunie. W przeciwieństwie do mousePressed, te funkcje są wywoływane raz. mousePressed zawsze zwróci jeden, dopóki myszka będzie naciśnięta. Podobnie ma się z klawiaturą: keyPressed() wywoła się raz, kiedy klawisz zostanie naciśnięty keyReleased() wywoła się raz, kiedy klawisz zostanie puszczony Funkcje te mogą tworzyć ciekawe kombinacje z funkcjami loop(), noLoop() I redraw(); jako że funkcja draw() wykonuje się za każdym razem, kiedy jest rysowana klatka programu, możemy to zatrzymać funkcją noLoop(). Powyższe funkcje przerwań dalej będą działać, więc redraw() zaktualizuje klatkę (narysuje ją, wykona kod w draw() tylko raz), a loop() spowoduje że program znowu zacznie się rysować. Do innych ciekawych funkcji należy noCursor(), który schowa kursor jeżeli będzie on w oknie programu. Można tak dzięki temu zrobić własne kursory. Funkcja cursor() przywróci widoczność kursora. Ba, możemy nawet podać wartość w funkcji cursor(), jak: ARROW, CROSS, HAND, MOVE, TEXT, WAIT aby zmienić ikonę kursora na np. klepsydrę lub łapkę. void setup() { size(200, 200); background(255); noStroke(); fill(0); rect(100,0,200,200); } void draw() { if (mouseX > 100) cursor(HAND); else cursor(ARROW); } Ostatnią, i chyba najważniejszą rzeczą, to funkcja save(). Zrobi ona migawkę z tego co właśnie wyświetla się na ekranie. Funkcja ta przyjmuje jeden argument, ścieżkę zapisu. Możemy także zapisać ponumerowane klatki (saveFrame), jeżeli chcemy zrobić z nich animację. Przydatna może być w takim wypadku funkcja frameRate(x), która ograniczy liczbę klatek na sekundę naszego programu. Po przyswojeniu sobie takiej dużej dawki wiedzy, proponuję zrobić kolejny praktyczny program, rysujący wykres wartości występujących w układzie RLC: Żeby nie komplikować sprawy, może to być wykres poglądowy (bez konkretnych jednostek). Program powinien być też responsywny, tj. dobrze funkcjonować przy zmianie rozmiaru okna (operuj na width i height!). Jeżeli ktoś nie rozumie co właśnie tutaj się znajduje, to proponuję napisać program rysujący wykres funkcji kwadratowej, lub chociaż liniowej, i wypisujący miejsca zerowe, współrzędne wierzchołka itd. Aby uzupełnić wszystko, pokażę jeszcze i omówię program z poprzedniej części, czyli odbijającą się piłeczkę. Przykładowy program mógł wyglądać tak: Niektórzy czytelnicy zapewne zauważyli, że w tym kodzie piłeczka się odbija, ale jakby od jej środka. Aby to naprawić, musimy uwzględnić promień piłki: Warto spostrzec, że w pierwszym przykładzie piłka poruszała się po stałym torze, natomiast w drugim jest ona bardziej nieprzewidywalna. Możemy oczywiście uwzględnić inne siły, takie jak opór powietrza, wytracanie energii po odbiciu, a nawet zasymulowanie praw dynamiki itd. - dokładnie to robią symulacje i gry. Więc jak widać, processing jest świetną aplikacją do robienia symulacji. W następnej części skończymy rozdział poświęcony pikselom w 2D, natomiast przeniesiemy się trochę do świata 3D i spróbujemy zrobić własny syntezator.







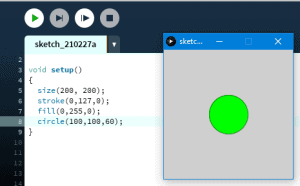




.gif.c2eeff64bb1936c2c56c51aeba1523ca.gif)