Kursy • Poradniki • Inspirujące DIY • Forum
Budując małego robota turniejowego nie przejmujemy się zbytnio jego wytrzymałością, bo to czego można się spodziewać roboty z pewnością wytrzymają. Wiadomo, że nadepnięcia przez człowieka raczej nie przeżyją, ale wystarczy, że będziemy ostrożni i nic złego ich nie spotka.
Jednak roboty walczące (sumo), czy różnego rodzaju łaziki i manipulatory, które z założenia mają wytrzymywać pewne obciążenia, należy dobrze przemyśleć. O ile czasami można to skutecznie zrobić na "czuja", to warto jednak poznać metody obliczeniowe, które dadzą nam pewność.
Wytrzymałość materiałów to dziedzina nauk inżynierskich opisująca zachowanie się konstrukcji pod wpływem obciążeń zewnętrznych.
Najważniejszym zagadnieniem wytrzymałości materiałów jest opis zależności pomiędzy siłami zewnętrznymi, a naprężeniami i odkształceniami które one wywołają w danej konstrukcji. Zależność tą w zakresie odkształceń sprężystych opisuje prawo Hooke'a.
Prawo Hooke'a
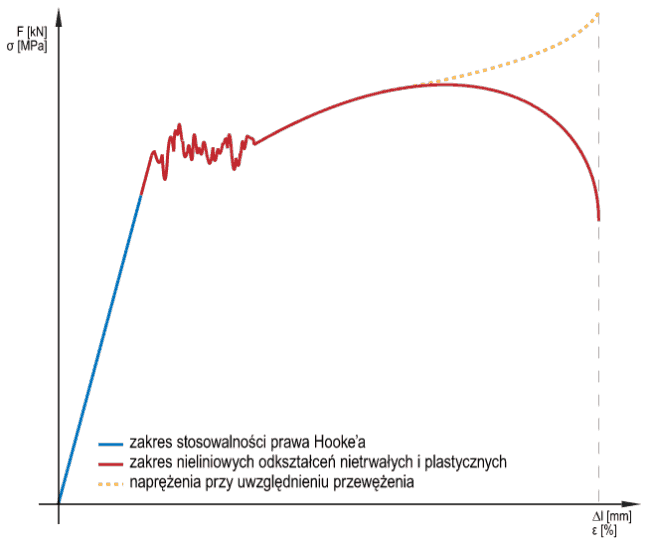
Prawo Hooke'a mówi o tym, że siła i odkształcenie są do siebie wprost proporcjonalne, a współczynnikiem proporcjonalności jest współczynnik sprężystości (moduł Younga lub Kirchoffa). Najprostszym przykładem, w którym można to zaobserwować jest statyczne rozciąganie pręta.
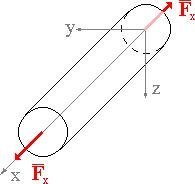
Wynikiem takiej próby przeprowadzonej na pręcie wykonanym ze stali niskowęglowej jest poniższy wykres. Oś pionowa reprezentuje przyłożoną siłę/naprężenie, a pozioma wydłużenie pręta/odkształcenie.
Zakres, który nas interesuje w kwestii wytrzymałości materiałów to ten zaznaczony na niebiesko. Jest to zakres odkształceń sprężystych materiału, czyli takich w którym po zaniku zewnętrznej siły, materiał wróci do swojej postaci.
W miejscu gdzie następuje zmiana z koloru niebieskiego na czerwony znajduje się granica sprężystości. Jeśli naprężenia przekroczą tą wartość to w materiale dojdzie do trwałych odkształceń. Chyba każdy z nas przekonał się o tym bawiąc się linijką na krawędzi stołu, naciskając ją delikatnie odginała się i sprężynując (denerwując przy tym nauczyciela) wróciła do swojego stanu początkowego, a jak się przesadziło to albo pękła (jeśli materiał był kruchy), albo się wygięła (materiał plastyczny).
Nie zawsze granica na wykresie jest tak wyraźna ("poszarpany" początek strefy odkształceń plastycznych - czerwony), często przejście z odkształceń sprężystych do plastycznych jest "gładkie", jednak aby korzystać z wartości takich jak moduł Younga czy granica sprężystości nie trzeba odczytywać ich z wykresu.
Są one podane w katalogach, normach, a co najważniejsze właściwości najpopularniejszych materiałów konstrukcyjnych są zawarte w bibliotekach oprogramowania CAD co później pokażę.
Wcześniej użyłem takich określeń jak naprężenie i odkształcenie. Naprężenie jest to stosunek siły do powierzchni na jaką ona działa. Wyróżniamy dwa rodzaje naprężeń.
Normalne, występują wtedy gdy siła działa prostopadle do płaszczyzny:
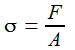
- F - siła [N]
- A - pole przekroju [mm^2]
Najczęściej stosowaną jednostką naprężeń jest MPa (megapaskal), czyli N/mm^2.
Odkształcenie względne jest to stosunek przyrostu długości do długości początkowej:
Gdzie:
- l - długość początkowa
- Δl - wydłużenie
Korzystając z tych parametrów prawo Hooke'a można zapisać tak:
Gdzie:
- E - moduł Younga [najczęściej podawany w GPa - gigapaskalach]
Podsumowując te wzory zauważamy, że pomiędzy naprężeniem, a odkształceniem występuje zależność liniowa. Dla przykładu: jeśli na drucie powiesimy 1kg i wydłuży się on o 1mm, to dokładając jeszcze 1kg (razem 2kg) wydłuży się on łącznie o 2mm.
Moduł Younga określa jak sztywny jest dany materiał. Drut który ma większy moduł Younga wydłuży się mniej niż ten z mniejszym modułem. Wartości dla przykładowych materiałów:
- guma - 0,1 GPa
- aluminium - 70 GP
- stal - 200 GPa
W obciążonym materiale występuje złożony układ naprężeń, który można rozbić na obciążenia proste, które potrafimy opisać:
- rozciąganie
- ściskanie
- zginanie
- docisk
- skręcanie
- ścinanie
Ścinanie i skręcanie generuje naprężenia ścinające, a pozostałe obciążenia - naprężenia normalne.
Każde z tych zjawisk mógłbym opisać dodatkowo jednak wydłużyłoby to artykuł. Wydaje mi się, że wiedza ta nie jest konieczna, aby z powodzeniem dokonywać obliczeń na komputerze, a to jest celem tego artykułu.
Dodam jedynie wyjaśnienie na temat docisku (inaczej nacisk) - jest to naprężenie występujące na powierzchni materiału wywołane przez siłę zewnętrzną np. cegła leżąca na stole oprócz tego, że powoduje ściskanie nóg stołu i zginanie jego blatu to także naciska na jego powierzchnię.
Warunek wytrzymałościowy
Kluczowym zagadnieniem całej analizy wytrzymałościowej jest spełnienie warunku:
Słownie rzecz ujmując naprężenia wywołane siłami zewnętrznymi nie powinny przekraczać naprężeń dopuszczalnych. Pytania jakie mogą się pojawić, to jakie naprężenia należy wziąć pod uwagę i ile wynoszą naprężenia dopuszczalne?
Naprężenie dopuszczalne to naprężenie niebezpieczne, czyli takie które spowoduje trwałe uszkodzenie materiału (jest to granica sprężystości o której wspominałem podczas omawiania pierwszego wykresu) podzielone przez współczynnik bezpieczeństwa.
Gdzie:
- n - współczynnik bezpieczeństwa
Dobór współczynnika bezpieczeństwa nie jest zadaniem łatwym, gdyż możemy znaleźć tylko pewne wytyczne ile on powinien wynosić, a reszta to kwestia naszego doświadczenia inżynierskiego.
Jak można się domyślić musi mieć on wartość większą od 1. Stosuje się go ponieważ przede wszystkim nie możemy być 100% pewni wartości naprężeń niebezpiecznych, może się ona zmienić w wyniku np. jakości materiału. Nie jesteśmy również w stanie przewidzieć wszystkich warunków pracy projektowanej konstrukcji oraz należy wziąć pod uwagę fakt, że teoria jest pewnym przybliżeniem rzeczywistości i nie opisuje jej w sposób idealny, a również proces obliczeń czy to ręcznych, czy komputerowych jest obarczony zawsze jakimś błędem.
O ile założenie niskiego wsp. bezpieczeństwa stwarza zagrożenia dla konstrukcji, czy także dla ludzi to założenie zbyt wysokiego współczynnika wpływa na masę i gabaryty konstrukcji oraz jej cenę, ponieważ, aby obniżyć wartości naprężeń należy zwiększać przekroje.
Zakładam, że nikt bazując na tym artykule nie będzie projektował konstrukcji mogących zagrozić życiu ludzkiemu (np. maszyny latające czy windy), dlatego wypiszę kilka prostych wytycznych doboru współczynnika bezpieczeństwa:
- od 1,5 do 3 dla materiałów elastycznych
- od 8 do 12 dla materiałów kruchych
- dla obciążeń stałych można przyjmować niższe wartości (np. dla stali konstrukcyjnej n=2)
- dla obciążeń zmiennych należy przyjmować wyższe wartości
Istnieją również tabele zawierające wartości naprężeń dopuszczalnych dla obciążeń prostych (rozciąganie, zginanie, ścinanie). Jeśli badana przez ciebie konstrukcja podlega takim obciążeniom to z powodzeniem możesz z nich skorzystać. Wracając do naszego warunku to pozostaje jeszcze pytanie jakie naprężenie musi być mniejsze od dopuszczalnego. Problemu nie ma jeśli mamy np. samo rozciąganie czy samo zginanie. Jeśli jednak występuje wymieszanie tych obciążeń należy je zredukować do jednego za pomocą tego wzoru:
Problem całkowicie znika jeśli obliczeń dokonujemy w CAD'ach. Jak się później przekonacie wynikiem takich obliczeń jest rozkład naprężeń w badanym elemencie. Ciekawostką jest, że wzór ten jest wynikiem hipotezy opracowanej niezależnie przez polskiego uczonego Maksymiliana Hubera oraz Austriaka Richarda von Misesa, dlatego w Polsce mówi się o twierdzeniu Hubera-Misesa, a za granicą i w oprogramowaniu CAD te naprężenia są naprężeniami von Misesa.
Warto zwrócić również uwagę, że wynik tego równania będzie zawsze dodatni, a np. rozważając rozciąganie, jeśli zmienimy znak siły, czyli po prostu jej zwrot to otrzymamy ujemne naprężenia oznaczające po prostu ściskanie.
W naszym przypadku nie ma to większego znaczenia, ponieważ większość materiałów konstrukcyjnych ma taką samą wytrzymałość na ściskanie jak i rozciąganie.
Uważać należałoby np. badając konstrukcje betonowe, ponieważ wytrzymałość betonu na ściskanie jest dużo większa niż na rozciąganie.
Podsumowanie
Wydaje mi się, że zawarłem w tym telegraficznym skrócie najważniejsze informacje, które pozwolą na przeprowadzenie analizy wytrzymałościowej za pomocą oprogramowania CAD - tym zajmiemy się w drugiej części artykułu.
Zachęcam jednak do samodzielnego, dokładniejszego zapoznania się z tematem, ponieważ im lepiej rozumiemy teorię, tym łatwiej jest ją wykorzystywać w praktyce.
To nie koniec, sprawdź również
Przeczytaj powiązane artykuły oraz aktualnie popularne wpisy lub losuj inny artykuł »
CAD, materiały, symulacja, teoria, wytrzymałość







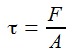
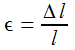
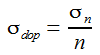
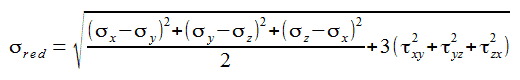











Trwa ładowanie komentarzy...