Kursy • Poradniki • Inspirujące DIY • Forum
Przed nami zdecydowanie najciekawsza (jak do tej pory) i najbardziej praktyczna część kursu. Pamiętaj, aby wszystkie doświadczenia wykonywać w praktyce – jest to kluczowe przy nauce elektroniki.
Czym jest prawo Ohma?
W pierwszej części kursu poznałeś podstawowe wielkości, którymi posługują się elektronicy. Jak łatwo się domyślić, są one ze sobą powiązane. Prąd, napięcie i rezystancję wiąże prawo Ohma, opisujące stosunek napięcia (przyłożonego do elementu) o danym oporze, w wyniku czego płynie prąd.
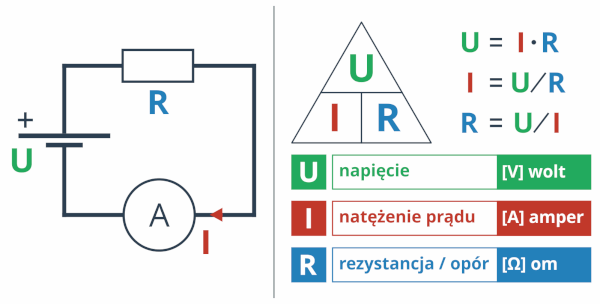
Zapamiętaj, że wielkości te oznaczamy zawsze następująco: U – napięcie, R – opór, I – prąd.
Z prawem tym w kontekście elektroniki będziesz spotykał się bardzo często. Na szczęście nie musisz uczyć się żadnej długiej regułki, ponieważ w najprostszej formie wyraża się ono trzema prostymi wzorami, które dla ułatwienia zazwyczaj zapisuje się w formie poniższej piramidki.
Jak korzystać z tej piramidki? Zasłaniamy wielkość, którą chcemy uzyskać, a ułożenie pozostałych wielkości podpowiada nam wzór. Informacje te znajdziesz również w materiałach dodatkowych do tego kursu (do ściągnięcia po rejestracji naszego zestawu), są one także częścią kieszonkowych ściąg.
Tak naprawdę jest to jeden wzór, przekształcony w zależności od potrzeb. Wystarczy zapamiętać jedną z form (np. U = I * R), aby w każdej chwili przekształcić ją w inną.
Interpretacja prawa Ohma
Zanim przejdziemy do przykładu, zastanówmy się, jak można zrozumieć te wzory. W odniesieniu do prądu prawo Ohma mówi, że jest on wprost proporcjonalny do przyłożonego napięcia. Przykładowo: jeśli zwiększymy napięcie 10 razy, to prąd również wzrośnie 10 razy. Wynika to jasno ze wzoru I = U / R (im wyższe będzie napięcie podstawione do wzoru, tym większy będzie prąd).
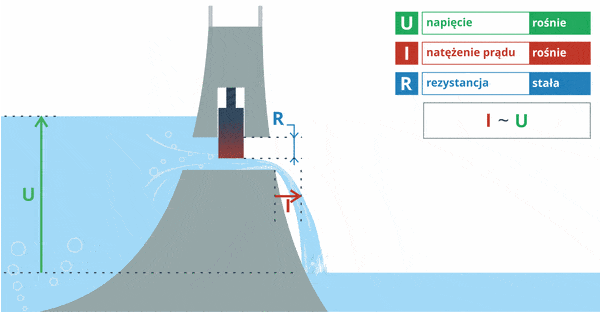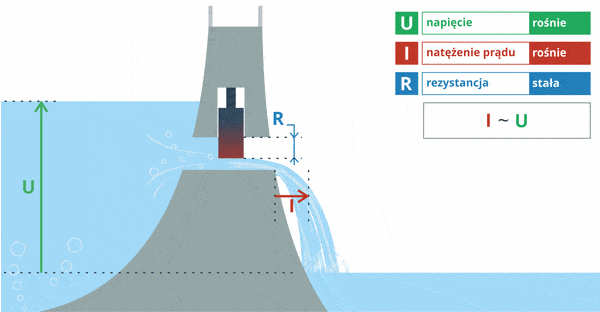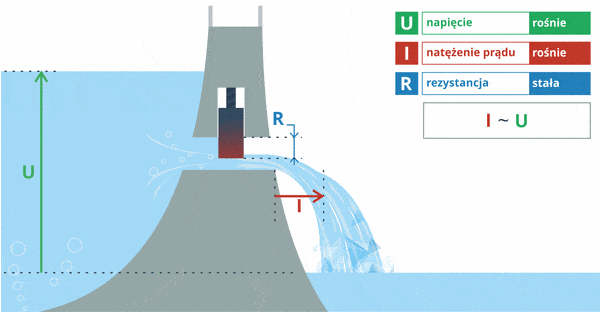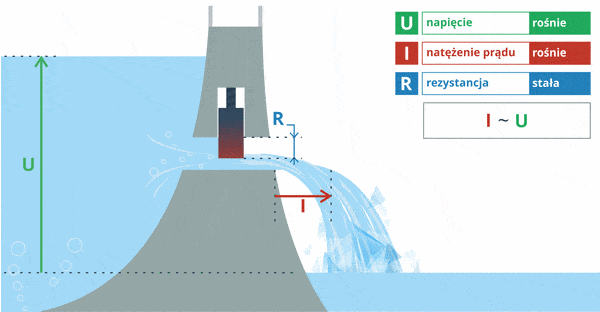
Pamiętasz naszą wodną analogię z początku kursu? Tam jest to doskonale widoczne: gdy poziom wody podniesie się (napięcie wzrośnie), to z tamy wypłynie więcej wody (wzrośnie prąd).
Jak widać, mamy tutaj zwiększające się napięcie (poziom wody) przy stałym oporze (położenie śluzy w tamie). Wniosek: wzrost napięcia prowadzi do przepływu większego prądu przy tym samym oporze.
Zapis I ~ U oznacza tutaj, że prąd jest wprost proporcjonalny do napięcia.
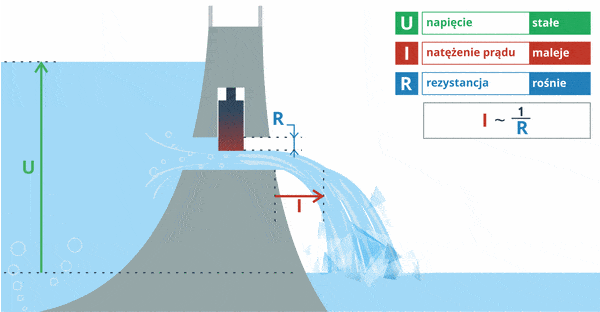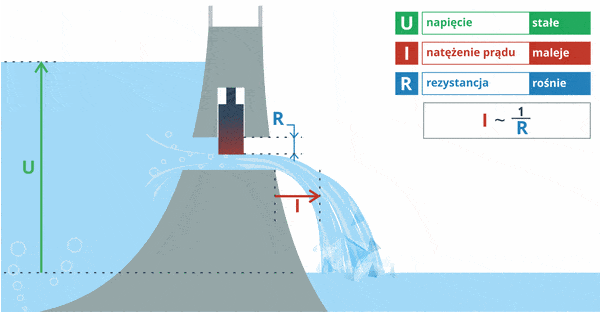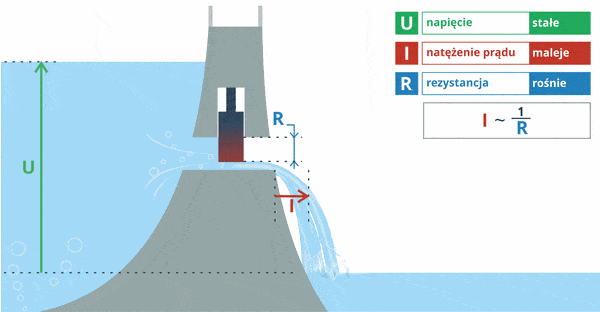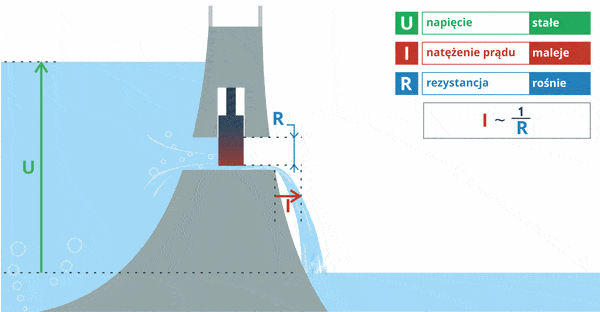
Rozważmy kolejny przykład. Tym razem poziom wody będzie stały (napięcie). Zmianie ulegać będzie jedynie stopień otwarcia śluzy w tamie (opór):
Tym razem możemy zaobserwować, że przy stałym napięciu prąd, który płynie przez dany element, zależy od jego oporu. Wniosek: prąd jest odwrotnie proporcjonalny do oporu (im mniejszy opór, tym większy prąd popłynie w układzie).
Zapis I ~ 1 / R oznacza tutaj, że prąd jest odwrotnie proporcjonalny do oporu.
Prawo Ohma w praktyce
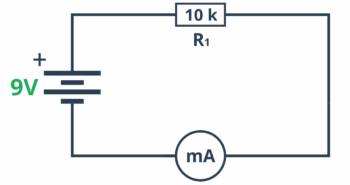
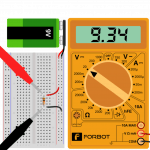
Sprawdźmy w praktyce, czy prawo Ohma naprawdę „działa”. W zestawie elementów znajduje się bateria o napięciu 9 V. Chcielibyśmy wiedzieć, jaki prąd popłynie, jeśli zamkniemy obwód, dołączając do niej rezystor 10 kΩ. Kółko z napisem „mA” symbolizuje na schemacie nasz multimetr ustawiony jako amperomierz, który (jak pisaliśmy w poprzedniej części kursu) wpinamy zawsze szeregowo.
Na początku sprawdzenie teoretyczne. Korzystamy z poznanych wcześniej wzorów:
U = 9 V, R = 10 kΩ, I = ?
I = U / R = 9 V / 10000 Ω = 0,0009 A = 0,9 mA
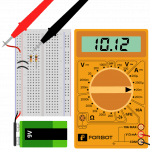
Powinniśmy spodziewać się około 0,9 mA. Teraz złóż na płytce stykowej powyższy układ. W razie problemów możesz posiłkować się poniższym przykładem. Uważaj tylko, aby wtykając elementy, nie zrobić nigdzie zwarcia, bo możesz rozładować lub uszkodzić baterię.
Pamiętaj, aby podczas pomiaru prądu ustawić odpowiednio multimetr!
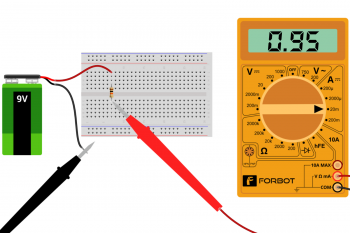
- Pomiar prądu płynącego przez rezystor 10k
- Szeregowe podłączenie miernika
Wynik pomiaru w powyższym układzie to 0,95 mA. Skąd ta rozbieżność? Nie wolno zapominać, że pomiar jest obarczony błędem. Po pierwsze, jak pamiętasz z poprzedniej części, rezystory są wykonane z pewną dokładnością (tutaj 5%) – to wprowadza największy błąd. Sprawa druga to opór przewodów pomiarowych oraz sam miernik, który również wykonuje pomiary z pewną dokładnością. Po trzecie Twoja bateria wcale nie daje dokładnie 9 V! Podsumowując: wynik jest poprawny!
Gotowe zestawy do kursów Forbota
Komplet elementów Gwarancja pomocy Wysyłka w 24h
Chcesz zrozumieć elektronikę? Zamów zestaw elementów do wykonania wszystkich ćwiczeń z kursu i przejdź do praktyki!
Zamów w Botland.com.pl »Taniej w pakiecie: Mistrz Elektroniki • Mistrz Majsterkowania
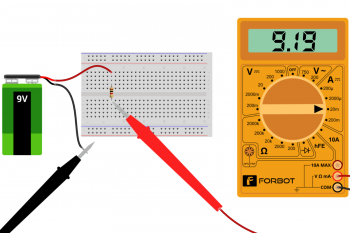
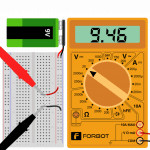
Teraz dla testu warto sprawdzić, co się stanie, jeśli zamiast rezystora 10 kΩ do układu wepniemy inny rezystor, a konkretnie 1 kΩ. Pamiętając o prawie Ohma, powinniśmy już przewidywać, że podłączenie rezystora o 10 razy mniejszym oporze powinno dać 10 razy większy prąd. Sprawdźmy:
Nie podłączaj teraz do układu losowych mniejszych rezystorów i nie dokonuj pomiaru prądu bez rezystora. Może wtedy popłynąć większy prąd, który uszkodzi bezpiecznik w mierniku.
Czym jest pierwsze prawo Kirchhoffa?
Prawo Kirchhoffa jest podzielone na dwie równorzędne części. Pierwsze prawo mówi, że tyle samo prądu wypływa z danego węzła, co do niego wpływa. Węzłem nazywamy miejsce, w którym łączą się przewody, ścieżki lub wyprowadzenia elementów.
Oznacza to m.in., że przez elementy połączone szeregowo popłynie ten sam prąd.
I prawo Kirchhoffa - skrót wideo »
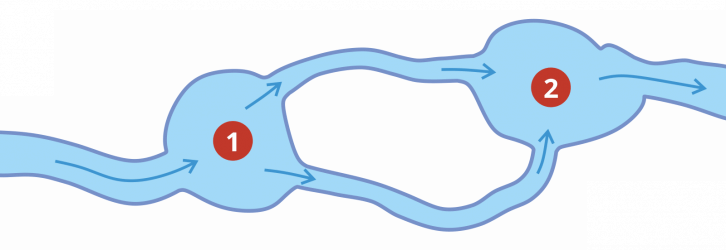
Posługując się analogią wodną, można to opisać jako przypadek, w którym rzeka wpływająca do jeziora (węzeł nr 1) rozgałęzia się na dwie mniejsze rzeczki wpływające do drugiego jeziora (węzeł nr 2). Intuicyjnie czujemy, że tyle samo wody dopływa do każdego z węzłów i tyle samo z nich wypływa.
Pierwsze prawo Kirchhoffa w praktyce
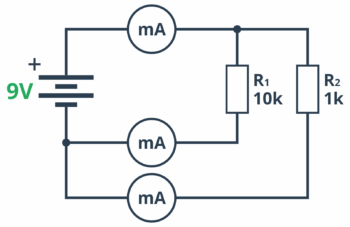
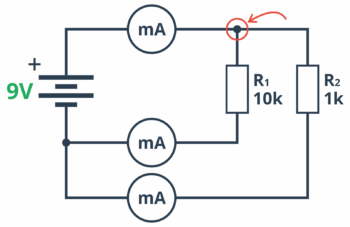
Prawo to można sprawdzić kolejnym doświadczeniem. Tym razem nie mamy czego liczyć, dlatego od razu budujemy układ na płytce stykowej. Będzie on trochę udziwniony. Chcemy podłączyć równolegle dwa rezystory, a następnie zmierzyć prąd pobierany przez każdy z nich oraz sumę prądów.
Oczywiście nie potrzebujemy trzech amperomierzy! Jednocześnie będziemy dokonywać tylko jednego pomiaru. Dlatego spokojnie możemy wykorzystywać do tego nasz multimetr, a na schemacie pokazano tylko miejsca, w które będziemy „wpinać się” miernikiem.
Na płytce stykowej można przykładowo zrealizować ten układ w taki sposób:
- Schemat montażowy układu
- Przykładowa realizacja w praktyce
Następnie wykonujemy odpowiednie pomiary:
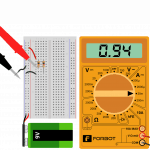
- Pomiar prądu w gałęzi z R=10k
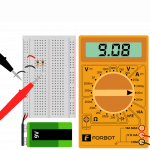
- Pomiar prądu w gałęzi z R=1k
- Pomiar prądu całego układu
Czy suma 0,94 + 9,08 daje nam 10,12 mA? Można powiedzieć, że tak – z dokładnością do 0,1 mA, co jest niewielkim błędem. Sumując prądy płynące przez dwa rezystory, otrzymujemy prąd pobierany z baterii. W naszym przypadku węzłem, w którym zachodzi sumowanie prądów, może być przykładowo ten zaznaczony poniżej na czerwono (ma on 1 wejście i 2 wyjścia):
Czym jest drugie prawo Kirchhoffa?
Z kolei drugie prawo Kirchhoffa odwołuje się do napięć na poszczególnych elementach układu. Mówi ono, że jeżeli wybierzemy w obwodzie dowolną drogę zamkniętą, to suma napięć pochodzących od źródeł zasilania jest równa sumie napięć na pozostałych elementach.
Nie martw się, jeśli powyższa definicja nie jest dla Ciebie zrozumiała. Najważniejsze, abyś zapamiętał, że na podzespołach połączonych równolegle zawsze będzie to samo napięcie, ponieważ są dołączone do tego samego zasilania. Natomiast przy elementach połączonych szeregowo suma napięć (spadków napięć) na poszczególnych elementach jest równa napięciu zasilającemu.
II prawo Kirchhoffa - skrót wideo »
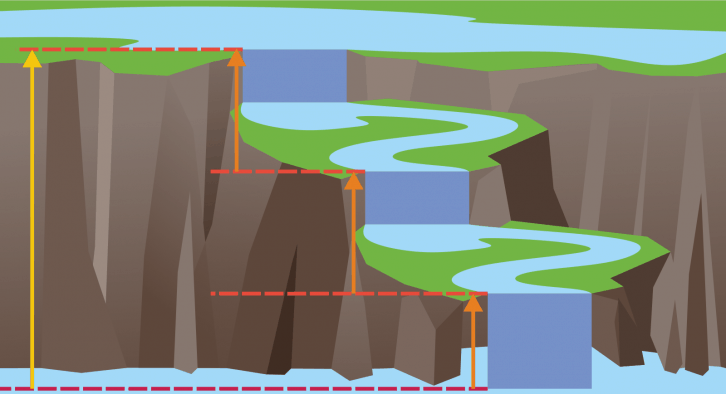
Posługując się analogią wodną, można przyrównać to do kilku małych wodospadów. Suma wysokości spadków wody na każdym z nich musi być równa wysokości całej kaskady wodospadów. Odnieśmy to do poniższej ilustracji – suma wysokości zaznaczonych na pomarańczowo jest równa wysokości, która została zaznaczona na żółto:
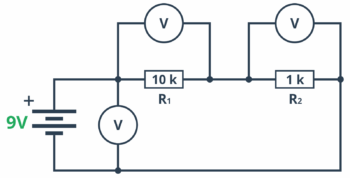
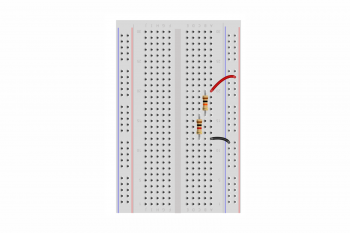
Najlepiej sprawdzić to w praktyce. Tym razem do baterii 9 V podłączmy szeregowo dwa rezystory (1 kΩ oraz 10 kΩ). Następnie mierzymy napięcie po kolei w trzech miejscach:
- spadek napięcia na rezystorze 1 k,
- spadek napięcia na rezystorze 10 k,
- napięcie na zaciskach baterii 9 V.
Schemat układu:
W celu pomiaru spadku napięcia na danym elemencie należy jedną sondę woltomierza przyłożyć przed elementem, a drugą za nim!
Układ na płytce stykowej może wyglądać następująco:
- Połączenie układu na płytce
- Przykładowe połączenie w praktyce
W praktyce układ jest prosty. Najważniejsze, aby sondy pomiarowe przykładać we właściwych miejscach i odpowiednio podłączyć baterię 9 V. Przykładowe pomiary:
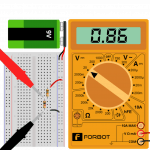
-
Pomiar spadku
napięcia na R=1k
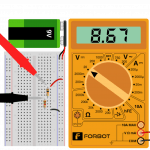
-
Pomiar spadku
napięcia na R=10k
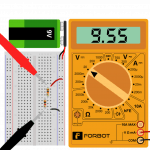
-
Pomiar spadku
napięcia na całym układzie
Sprawdźmy teraz wyniki, sumując zmierzone napięcia: czy 0,86 + 8,67 to 9,55? Tak, z dokładnością do 0,02 V. Taki błąd jest dopuszczalny, ponieważ wynika z niedoskonałości sprzętu pomiarowego oraz użytych elementów.
Czym jest dzielnik napięcia?
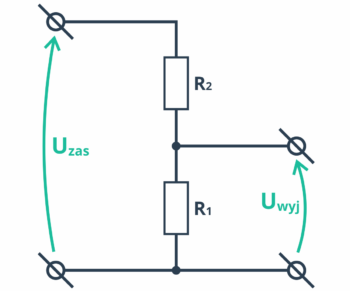
Zwróć szczególną uwagę na ten fragment, który opisuje bardzo często używane połączenie dwóch rezystorów! Dzielnik napięcia to nic innego jak jedno z praktycznych zastosowań powyższych praw. W praktyce wszystko jest banalnie proste – łączymy dwa rezystory szeregowo i zasilamy je.
Napięcie na zaciskach każdego z nich będzie proporcjonalnie mniejsze, ale ich suma będzie równa napięciu zasilania. Jest to nic innego jak ilustracja działania drugiego prawa Kirchhoffa. Inaczej mówiąc, układ ten pozwala podzielić nam napięcie zasilania, dzięki czemu z baterii 9 V możemy otrzymać np. 6 V.
Opisuje się to następującym wzorem:
Uzas to napięcie zasilające nasz dzielnik. W liczniku wstawia się wartość rezystora, na którym chcemy poznać spadek napięcia. W mianowniku znajduje się suma obu rezystancji. Takie połączenie już robiliśmy, więc nie będziemy go teraz powtarzać – najważniejsze, aby pamiętać o wzorze pozwalającym nam obliczyć napięcie, które powinno pojawić się na rezystorze.
Dzielnik napięcia - skrót wideo »
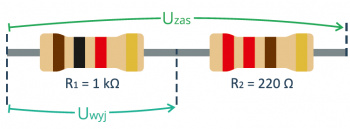
Dla przykładu policzmy, jaką wartość napięcia uzyskamy na dzielniku składającym się z rezystorów 1 kΩ oraz 220 Ω (specjalnie dobrany został taki, jakiego nie ma w zestawie), zasilanym 3 V. Układ ten będzie wyglądał następująco:
Obliczenie napięcia Uwyj będzie w tym przypadku wyglądało następująco:
Teraz wykonaj samodzielnie obliczenia dla dzielnika składającego się z rezystorów 1 kΩ oraz 330 R, zasilanego 9 V. Oblicz Uwyj mierzone na rezystorze 1 kΩ. Sprawdź później, czy wynik zgadza się z praktyką – zbuduj samodzielnie taki układ na płytce stykowej i zmierz napięcie. W razie problemów wróć do ćwiczenia wykonanego przy demonstracji drugiego prawa Kirchhoffa.
Dlaczego jest to bardzo praktyczne?
W świecie elektroniki popularne są czujniki, z których zmierzone wartości fizyczne odczytuje się, mierząc opór czujnika, np. opór analogowego czujnika temperatury zależy od temperatury otoczenia.
Mikrokontrolery (np. te używane w Arduino) nie potrafią mierzyć zmian rezystancji. Świetnie radzą sobie jednak z pomiarem napięcia. Jeśli w naszym dzielniku napięcia rezystor R1 zastąpimy takim czujnikiem, to zmiany temperatury będą zamieniane właśnie na zmiany napięcia. Takie połączenie jest bardzo popularne. Używamy go np. w kursie programowania Arduino, ale pojawia się też podczas ćwiczeń wykonywanych w ramach drugiego poziomu kursu elektroniki:
Czujniki analogowe w kursie elektroniki (poziom II)
Układy elektroniczne odbierają bodźce ze świata zewnętrznego poprzez różnego rodzaju czujniki (sensory). Pomiar temperatury, natężenia... Czytaj dalej »
Uwaga! Dzielniki napięcia nie służą jednak do zasilania układów. Nie możesz wykorzystać takiego dzielnika do tego, aby z baterii 9 V zasilić układ wymagający 5 V. Nie można też za ich pomocą zasilać np. silników (a wielu początkujących uważa to za dobry pomysł). Z dzielników napięcia nie można pobierać dużego prądu! Do zasilania takich układów należy zastosować stabilizatory napięcia, które zostaną omówione w dalszej części kursu.
Czym są potencjometry?
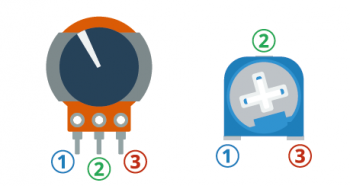
Potencjometry to rezystory z regulowaną wartością oporu. Kręcąc główką potencjometru, wpływamy na jego opór mierzony między środkową a skrajną nóżką. Przykładowe potencjometry:
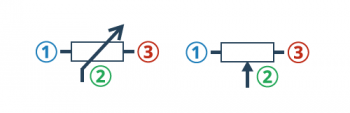
Potencjometry na schematach są przedstawiane na dwa sposoby (symbol nie jest związany z typem elementu):
Zależnie od wersji obudowy nóżki mogą być rozmieszczone w różny sposób, ale zawsze da się łatwo wyróżnić środkowe wyprowadzenie, a to jest najważniejsze:
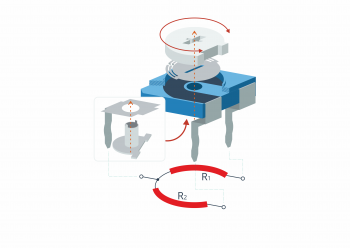
Potencjometry to bardzo sprytne dzielniki napięcia: po ścieżce o stałej rezystancji porusza się suwak z dobrze przewodzącego materiału, dzielący ją na dwa rezystory. Dlatego schemat „zastępczy” tego elementu może wyglądać następująco:
Całość w środku wygląda mniej więcej tak jak poniżej – rezystory zaznaczone na czerwono to tylko symboliczne przedstawienie tego, że suwak dzieli ścieżkę o stałej rezystancji na dwie części (jedna skrajna nóżka + środkowa i druga skrajna nóżka + środkowa).
Suma rezystancji dwóch tak uzyskanych rezystorów jest stała, ale zmienia się wartość rezystora, na którym odkłada się interesujące nas napięcie. Między skrajnymi nóżkami rezystancja jest stała, środkowa to odczep, czyli wyjście naszego rezystora o zmiennym oporze.
Dla łatwiejszego zrozumienia tematu poniżej widoczny jest rozłożony potencjometr montażowy:
-
Widok od spodu (pokrętło połączone
ze środkową nóżką)
-
Rozłożone elementy
potencjometru
-
Widok od góry z czarną
ścieżką o stałej rezystancji
Ponadto potencjometr może posłużyć jako rezystor o regulowanej rezystancji – wystarczy użyć jednego ze skrajnych odczepów i suwaka. Sprawdźmy teraz oba zastosowania w praktyce.
Potencjometr w praktyce – regulowany rezystor
Umieśćmy potencjometr w płytce stykowej i zmierzmy opór między środkowym wyprowadzeniem oraz dowolnym innym. Po przekręceniu białej główki potencjometru opór powinien się zmienić.
- Pomiary oporu potencjometru
- Ponowny pomiar przy innym ustawieniu
Potencjometr w praktyce – dzielnik napięcia
Teraz sprawdźmy, jak potencjometr sprawdza się w roli dzielnika napięć. Do skrajnych wyprowadzeń elementu podłączamy zasilanie z baterii (biegunowość nie robi różnicy), a następnie mierzymy napięcie między środkowym wyprowadzeniem oraz dowolną skrajną nóżką. Pamiętaj o odpowiednim ustawieniu miernika (teraz mierzymy napięcie). Po chwili przekręcamy białą główkę potencjometru i robimy drugi pomiar. Uzyskane wyniki mogą wyglądać następująco:
- Pomiar napięcia
- Ponowny pomiar napięcia
Czym jest opór wewnętrzny?
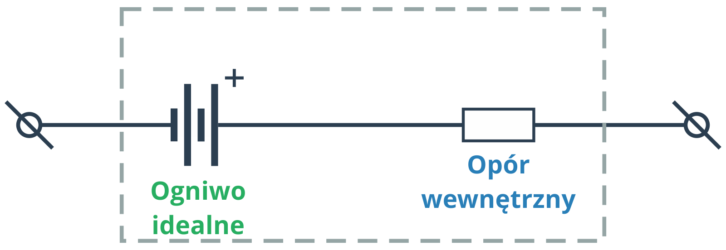
Opór wewnętrzny to parametr, którym cechuje się każde źródło zasilania, ale o którym często się zapomina. Każde rzeczywiste źródło napięcia można modelować, w najprostszym przypadku, jako szeregowe połączenie źródła idealnego i pewnej rezystancji.
Najprościej wyobrazić sobie, że wewnątrz baterii znajduje się rezystor.
Tej rezystancji nikt nie chce, ale „ona tam jest” i nie da się z tym nic zrobić; producenci mogą się tylko starać, aby ten opór był jak najmniejszy. Wynika to ze złożenia rezystancji kontaktów, okładek baterii, doprowadzeń itd. Poza tym opór potrafi zależeć od temperatury, wieku ogniwa i innych czynników.
Rezystancji tej nie można dokładnie obliczyć ani zmierzyć – nie próbuj jej zmierzyć, przykładając miernik w trybie pomiaru oporu do baterii, bo możesz go wtedy uszkodzić! Taką informację może nam jedynie podać producent (w przypadku zwykłych baterii jest to trudne do znalezienia). Na szczęście ta wartość nie jest dla nas teraz istotna, najważniejsze, żeby zdawać sobie tylko sprawę z jej istnienia.
Na tym etapie nauki wystarczy, że zapamiętasz fakt istnienia takiego zjawiska!
Obecność oporu wewnętrznego obrazuje bardzo proste doświadczenie. Zmierzmy napięcie w układzie, gdy prąd płynie przez rezystory 1 k oraz 10 k. Dodatkowo sprawdźmy, co się stanie, gdy w układzie nie będzie rezystora. Bardzo prosty układ pomiarowy:
- Schemat montażowy
- Przykładowa realizacja
Przykładowe wartości pomiarów:
- Podłączony rezystor 1k
- Podłączony rezystor 10k
- Brak rezystora
Jak widać na powyższym przykładzie, pobierając z baterii większy prąd, będziemy otrzymywać mniejsze napięcie. Doskonale można to wyjaśnić, używając dzielnika napięcia: im mniejszy jest R1 (będący obciążeniem) w stosunku do R2 (będącego oporem wewnętrznym), tym większe napięcie odkłada się na R2. Dla wielu osób zastanawiający może być pomiar bez rezystora, bo wydaje im się, że oznacza to brak oporu – to błędne myślenie. Brakiem oporu byłoby zastąpienie elementu przewodem.
Brak rezystora należy rozumieć jako nieskończenie wielki opór. Dlatego w układzie prąd nie płynie, a bateria nie jest w żaden sposób obciążona, więc zmierzone napięcie jest największe.
Pamiętaj, że obciążając baterię zbyt dużym prądem (poprzez rezystor o małej rezystancji lub zwarcie), można doprowadzić do jej rozgrzania, a nawet uszkodzenia, co spowoduje wylanie elektrolitu! Pobierając duży prąd, należy używać źródła o odpowiednio małym oporze wewnętrznym i odpowiednio dużej pojemności.
Powyższe zjawisko przeszkadza wielu początkującym, którzy chcą zasilać swoje roboty małymi bateriami (np. 9 V). Zapominają oni, że pobór dużego prądu (np. przez silniki) powoduje spadki napięcia na baterii. Może to uniemożliwić pracę całego układu.
Jak działają zasilacze stabilizowane?
Nasz eksperyment pokazał, że napięcie źródła zasilania zależy od prądu pobieranego z układu. Jeśli pobierany prąd jest stosunkowo duży, to napięcie na baterii może znacznie spaść. Jak w takim razie działają stabilizowane zasilacze, które dostarczają stabilną wartość napięcia niezależnie od obciążenia?
W zasilaczach stabilizowanych sprawa wygląda nieco inaczej: wbudowany tam układ stabilizujący bez przerwy porównuje napięcie na zaciskach z napięciem żądanym przez użytkownika i „doregulowuje” je, jeżeli jest za niskie. Stąd rezystancja wewnętrzna takich zasilaczy potrafi być wielokrotnie mniejsza niż nawet dużych akumulatorów. Więcej o tym w dalszej części, gdy zajmiemy się stabilizatorami:
Stabilizator napięcia w kursie elektroniki
Po raz pierwszy w kursie elektroniki odchodzimy od podstawowych elementów elektronicznych, by zająć się bardziej złożonymi układami. Istnieje... Czytaj dalej »
Pora na quiz - sprawdź, co już wiesz!
Przygotowaliśmy aż 4 quizy, dzięki którym sprawdzisz jak dużo zapamiętałeś z tego kursu elektroniki. Masz już za sobą trzy pierwsze odcinki kursu, więc śmiało możesz zabrać się za pierwszy quiz, który składa się z 15 pytań testowych (jednokrotnego wyboru), limit czasu to 15 minut. Liczy się pierwszy wynik, ale quiz będziesz mógł później wykonać wielokrotnie (w ramach treningu).
Bez stresu! postaraj się odpowiedzieć na pytania zgodnie z tym co wiesz, w przypadku ewentualnych problemów skorzystaj ze swoich notatek. To nie są wyścigi - ten quiz ma pomóc w utrwaleniu zdobytej już wiedzy i wyłapaniu ewentualnych tematów, które warto jeszcze powtórzyć. Powodzenia!
Quiz - najnowsze wyniki
Oto wyniki 10 osób, które niedawno wzięły udział w quizie. Teraz pora na Ciebie! Uwaga: wpisy w tej tabeli mogą pojawiać się z opóźnieniem, pełne wyniki są dostępne „na żywo” na stronie tego quizu.
| # | Użytkownik | Data | Wynik |
|---|---|---|---|
| 1 | Cisiu97 | 26.04.2024, 08:26 | 100%, w 117 sek. |
| 2 | m4cieg | 25.04.2024, 15:44 | 100%, w 285 sek. |
| 3 | bartek03 | 25.04.2024, 08:03 | 93%, w 171 sek. |
| 4 | daniel-krejci | 26.04.2024, 13:52 | 93%, w 196 sek. |
| 5 | Bartholomaeus | 25.04.2024, 11:49 | 93%, w 228 sek. |
| 6 | Giovanni101 | 26.04.2024, 00:21 | 93%, w 301 sek. |
| 7 | Paradoks | 26.04.2024, 20:18 | 93%, w 785 sek. |
| 8 | udhxbzbzjaiak | 25.04.2024, 09:00 | 20%, w 27 sek. |
| 9 | wojtekpozdro | 25.04.2024, 09:06 | 20%, w 48 sek. |
| 10 | Szymonek225 | 25.04.2024, 09:04 | 13%, w 361 sek. |
Podsumowanie
Za nami kolejna część kursu elektroniki. Tym razem trochę dłuższa, ale i tak było to ekspresowe tempo jak na omówienie najważniejszych praw rządzących światem elektroniki! W razie problemów śmiało pytaj w komentarzach – będziesz miał później duże kłopoty, jeśli nie zrozumiesz teraz tych zależności.
Będzie nam również bardzo miło, jeśli podzielisz się wynikami swoich eksperymentów i napiszesz w komentarzach, czy wszystko przebiegło bez problemów. Jeśli udało Ci się odpowiednio wykorzystać elementy z naszych zestawów, to śmiało idź do kolejnej części kursu i poznaj kondensatory!
Nawigacja kursu
Aktualna wersja kursu: Damian Szymański, ilustracje: Piotr Adamczyk. Pierwsza wersja: Michał Kurzela. Schematy montażowe zostały wykonane przy częściowym wykorzystaniu oprogramowania Fritzing (oraz własnych bibliotek elementów). Zakaz kopiowania treści kursów oraz grafik bez zgody FORBOT.pl
Data ostatniego sprawdzenia lub aktualizacji tego wpisu: 18.03.2024.
Powiązane wpisy
elektronika, kirchhoff, kursElektroniki, ohm, potencjometr, prawo, rezystory, teoria













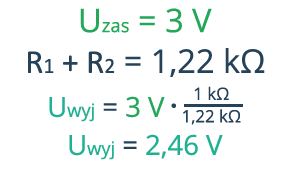


























Trwa ładowanie komentarzy...