Kursy • Poradniki • Inspirujące DIY • Forum
Na początek niezbędne jest wprowadzenie nowych pojęć i odrobiny teorii. Opisany tutaj materiał będzie wykorzystywany w kolejnych artykułach. Ważne jest zrozumienie tych podstaw, aby później nikt się nie dziwił dlaczego piszemy np. 1 + 1 = 1 - zachęcam do lektury!
Czym jest algebra Boole'a?
Ogólnie algebrą nazwiemy zbiór określonych elementów (np. liczb) oraz działań, które można na nich wykonywać. Przykładowo, każdy z nas posługuje się algebrą liczb rzeczywistych. Zawiera ona nieskończenie wiele liczb. Można na nich wykonywać operacje takie jak np. dodawanie, odejmowanie, mnożenie, czy dzielenie.
Komputery i inne urządzenia cyfrowe wykorzystują tylko dwie wartości: 0 (zero) i 1 (jeden). Te cyfry również można dodawać, odejmować, mnożyć, czy dzielić. Jednak tutaj wyniki mogą być inne! Zestaw tych wartości i operacji nazywamy właśnie tytułową algebrą Boole'a. Angielski matematyk George Boole opracował jej zasady już w XIX wieku.
Informacje na temat algebry Boole'a zostały opisane, w dalszej części artykułu,
z pominięciem informacji zbędnych dla początkujących elektroników.
Do czego może się przydać w elektronice taka uproszczona algebra? Na przykład do opisania:
- stanu przycisku, np. wciśnięty (1) lub puszczony (0),
- stanu wyjścia układu - jest napięcie (1), nie ma napięcia (0).
Jest to symboliczny, umowny sposób, który pozwala w szybki i łatwy sposób przedstawić różne informacje w świecie komputerów i elektroniki cyfrowej.
Krótki słownik pojęć
Podczas całej serii artykułów będziemy posługiwać się nowymi pojęciami, które są często używane zamiennie. Dlatego już teraz warto zapamiętać, że następujące pojęcia są równoważne:
1 = jedynka = logiczna jedynka = stan wysoki = prawda
0 = zero = logiczne zero = stan niski = fałsz
Dodatkowo, pojedyncze wartości (0 lub 1) będziemy nazywać bitami.
Bit nazywany jest również jednostką logiczną, ponieważ jest to najmniejsza ilość informacji wystarczająca do opisania stanu przyjętego przez układ. Dokładnie tak, jak było to wspomniane wcześniej - za pomocą jednego bitu możemy opisać stan przycisku (wciśnięty/puszczony), stan wyjścia układu (np. dioda włączona/wyłączona) itd.
Zastosowanie takie jest zapewne intuicyjne dla wszystkich, którzy spotkali się z liczbami binarnymi, programowaniem (np. Arduino) lub ogólnie mają styczność z informatyką. Pozostali na pewno szybko przyswoją te informacje podczas dalszych ćwiczeń praktycznych.
Gotowe zestawy do kursów Forbota
Komplet elementów Gwarancja pomocy Wysyłka w 24h
Części pozwalające wykonać ćwiczenia z kursu techniki cyfrowej dostępne są w formie gotowych zestawów! W komplecie m.in. niezbędne układy scalone CMOS, przewody połączeniowe, diody, buzzer, kontaktron, wyświetlacz 7-segmentowy oraz znacznie więcej!
Zamów w Botland.com.pl »Podstawowe reguły algebry Boole'a
Mamy do dyspozycji tylko dwie cyfry, za to bardzo charakterystyczne. Zero (0) jest znane jako element neutralny dodawania (nie zmienia jego wyniku), a jeden (1) nie wpływa na wynik mnożenia. Dodatkowo, mnożenie przez zero zawsze da w rezultacie zero.
Powyższe zasady można opisać takimi równaniami (a oznacza 0 lub 1):
a · 1 = a
a + 0 = a
a · 0 = 0
Sprawdźmy to podstawiając za a różne wartości:
0 · 1 = 0
0 + 0 = 0
0 · 0 = 0
1 · 1 = 1
1 + 0 = 1
1 · 0 = 0
Zależności te będą spełnione dla dowolnych liczb. Sprawdź sam, jeśli nie wierzysz!
Podobnie, jak zero determinuje wynik mnożenia, tak w takiej algebrze Boole'a jedynka przesądza o wyniku sumowania. Dodanie 1 do jakiejkolwiek liczby zawsze da w efekcie 1.
a + 1 = 1
To jest nowość, która dla wielu wydaje się być nieintuicyjna: wprawdzie 1 + 0 = 1, ale już 1 + 1 = 2. Potwierdzi to każdy - nawet dziecko w szkole podstawowej. Jednak algebra Boole'a zawiera tylko dwa możliwe stany (0 lub 1), dlatego 1 + 1, będzie tutaj równało się 1 - taka jest największa wartość jaką możemy wykorzystywać. Dlatego 1 + 1 + 1 nadal będzie równało się 1.
Jeśli w tej chwili jest to mało zrozumiałe, to spokojnie proponuję
czytać dalej. Całość wyjaśni się podczas przykładów praktycznych.
Reprezentacja wartości logicznych w praktyce
Wartości 0 oraz 1 są pojęciami czysto abstrakcyjnymi - tak samo, jak wszystkie inne liczby. Na co dzień posługujemy się czymś, co je reprezentuje.
Dla stanów logicznych w układach cyfrowych są to
napięcia o odpowiednich wartościach.
W ramach niniejszego kursu, będziemy posługiwać się układami cyfrowymi z rodziny CMOS. Ich struktury oparte są o tranzystory unipolarne (jak pewnie pamiętasz, sterowanie tymi elementami przebiega napięciowo, a nie prądowo, jak w tranzystorach bipolarnych).
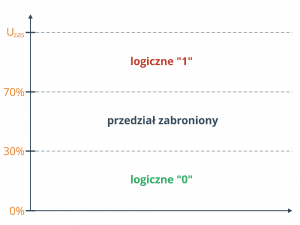
Producenci ustalili, że poziomy logiczne będą reprezentowane następująco:
- 0% - 30% napięcia zasilania oznacza logiczne zero (0),
- 30% - 70% napięcia zasilania jest przedziałem zabronionym,
- 70% - 100% napięcia zasilania oznacza logiczną jedynkę (1).
Dla nas oznacza to tyle, że wymuszenie stanu logicznego 0 sprowadza się do podłączenia danego wejścia do masy zasilania. Jeżeli chcemy podać na dane wejście stan 1, trzeba je podłączyć do dodatniego bieguna zasilania.
Nie jest to jedyny sposób rozróżniania w elektronice 0 od 1.
Metoda ta jest jednak obecnie najpopularniejsza!
Na nasze potrzeby, będziemy wykorzystywać następujące reprezentacje stanów logicznych:
Zero:
- podłączenie do masy,
- brak świecenia diody,
- świecenie diody zielonej (jeśli do danego wyjścia jest podłączona czerwona i zielona),
- brak wciśnięcia przycisku.
Jeden:
- podłączenie do dodatniego bieguna zasilania,
- świecenie diody,
- świecenie diody czerwonej (jeśli do danego wyjścia jest podłączona czerwona i zielona),
- wciśnięcie przycisku.
Będą one wykorzystywane we wszystkich częściach tego kursu.
Operacje na bitach, czyli funktory
Operacje bitowe (nazywane inaczej: funktorami) noszą swoje własne, specyficzne nazwy, którymi będziemy się posługiwać. Przed przejściem do układów cyfrowych warto zbudować opisane tutaj funktory samodzielnie. W tym celu wykorzystamy najprostsze możliwe elementy elektroniczne, które zostały opisane podczas kursu elektroniki (poziom I).
W przykładach wejścia układu (zera lub jedynki) symbolizowane są przez przyciski.
Wyjście układu (stan wysoki lub niski) widoczne jest na diodzie świecącej.
Negacja, zaprzeczenie - NOT
Negacja (zwana również zaprzeczeniem) jest operacją, która przyjmuje tylko jeden argument. W wyniku jej działania otrzymujemy wartość przeciwną. Wynikiem zaprzeczenia "prawdy" będzie "fałsz" i odwrotnie, negacją "fałszu" będzie "prawda".
Negację oznacza się symbolem tyldy (~) lub w postaci funkcji, jako NOT():
~0 = NOT(0) = 1
~1 = NOT(1) = 0
Możemy, to zapisać w formie tabelki. Lewa kolumna, to wartość przed wykonaniem danej funkcji (tutaj negacji), a prawa kolumna, to wynik tej funkcji.
Do takiej formy zapisu (w tabeli) wrócimy w 3 części kursu.
Już teraz warto się do niego przyzwyczajać!
Sprawdźmy, jak negacja "wygląda" w praktyce, tym razem potrzebne będą:
- płytka stykowa,
- przycisk,
- rezystor 1kΩ,
- czerwona dioda świecąca,
- przewody połączeniowe,
- 4 baterie AA w koszyku.
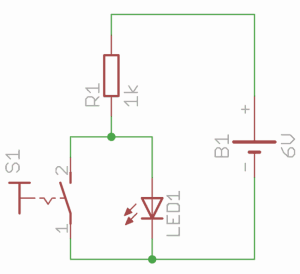
Wszystkie elementy są częścią dostępnych zestawów. Powyższe części należy połączyć zgodnie z następującym schematem:
Po włączeniu zasilania czerwona dioda będzie świecić - zgaśnie po wciśnięciu przycisku. Stanie się tak, ponieważ cały prąd wypływający z R1 będzie odprowadzany przez styki S1 do masy.
Według omówionych reguł mamy tutaj negację stanu przycisku.
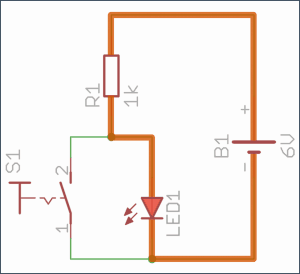
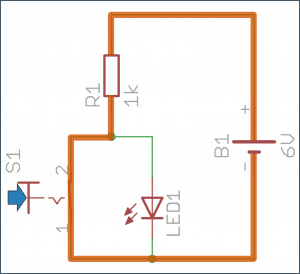
Pomarańczowa linia wskazuje, którą drogą w danej sytuacji popłynie większość prądu:
- Przycisk puszczony (0) – dioda świeci (1).
- Przycisk wciśnięty (1) – dioda nie świeci (0).
Działanie układu w praktyce widoczne jest na poniższych zdjęciach:
- Przycisk puszczony (0) – dioda świeci (1).
- Przycisk wciśnięty (1) – dioda nie świeci (0).
Suma logiczna, alternatywa - OR
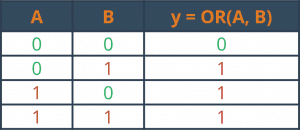
Suma logiczna (inaczej alternatywa) wymaga dwóch argumentów. Gdy przynajmniej jeden z nich ma wartość 1, to wtedy wynik całej funkcji ma wartość 1. W przeciwnym razie, wynik jest zerowy. Operację tę oznacza się symbolem plusa (+) lub pisząc OR.
0 OR 0 = 0
1 OR 0 = 1
1 OR 1 = 1
Ostatni przykład można przyrównać do sumowania "prawdy" z "prawdą". Nie wyjdzie z tego "podwójna prawda", ani prawda bardziej prawdziwa. To jest po prostu "prawda".
Uniwersalny zapis w formie tabelki:
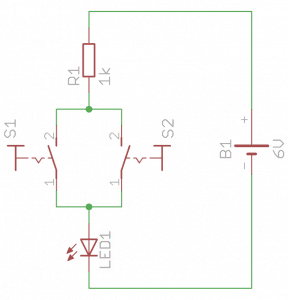
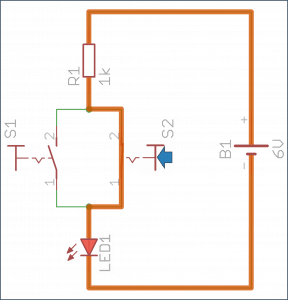
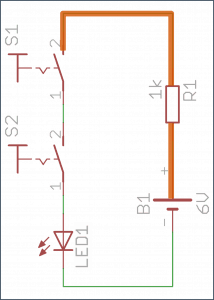
Pora, aby sprawdzić jak działa sumowanie zgodne z algebrą Boole'a. Do poprzedniego przykładu wystarczy dodać jeden przycisk. Dokładnie tak, jak na poniższym schemacie:
Wciśnięcie przynajmniej jednego przycisku spowoduje świecenie diody. Zwarcie większej liczby styków niczego nie zmieni (ich rezystancja jest pomijanie mała). Działanie tego układu w praktyce widoczne jest na poniższych 4 zdjęciach:
- Oba przyciski puszczone – dioda wyłączona.
- Pierwszy przycisk wciśnięty – dioda świeci.
- Drugi przycisk wciśnięty – dioda świeci.
- Oba przyciski wciśnięte – dioda świeci.
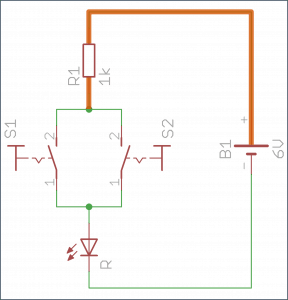
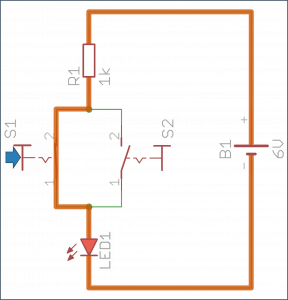
Pomarańczowa linia wskazuje, którą drogą w danej sytuacji popłynie prąd:
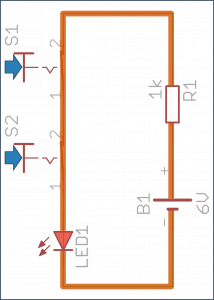
- Oba przyciski puszczone – dioda wyłączona.
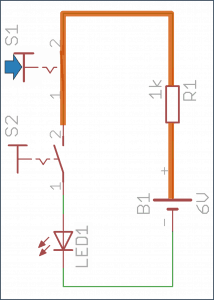
- Pierwszy przycisk wciśnięty – dioda świeci.
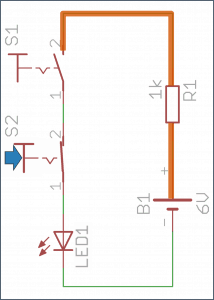
- Drugi przycisk wciśnięty – dioda świeci.
- Oba przyciski wciśnięte – dioda świeci.
Według omówionych reguł mamy tutaj sumę logiczną dwóch wejść.
Sumę logiczną można rozszerzyć na większą liczbę argumentów, na przykład:
0 OR 0 OR 0 = 0
0 OR 1 OR 0 = 1
0 OR 1 OR 0 OR 1 OR 0 OR 1 OR 0 = 1
Teraz powinno być już jasne, dlaczego w algebrze Boole'a
dodawanie do siebie kilku jedynek daje nadal 1.
Niezależnie od tego, czy w powyższym przykładzie z sumą wciskalibyśmy 1, czy 10 przycisków (dodawanie 10 jedynek do siebie), to dioda świeciłaby zawsze tak samo, co symbolizowałoby cały czas na wyjściu układu wartość 1.
Iloczyn logiczny, koniunkcja - AND
Iloczyn logiczny (nazywany również koniunkcją) działa podobnie do znanego nam mnożenia: jeżeli wśród argumentów znajdzie się chociaż jedno 0, to wtedy cały wynik będzie zerowy. Symbolicznie zapisuje się je ampersandem (&), kropką (·) lub pisząc AND.
1 AND 1 = 1
1 AND 0 AND 1 AND 1 = 0
1 & 1 & 1 & 1 & 0 = 0
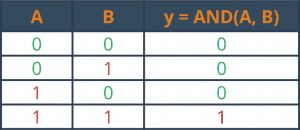
Uniwersalny zapis w formie tabeli:
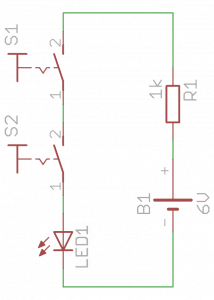
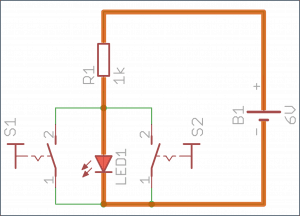
Działanie tej funkcji można odtworzyć na płytce stykowej korzystając z tych samych elementów, które zostały użyte wcześniej. Tym razem schemat wygląda następująco:
Przyciski są połączone szeregowo. Wciśnięcie tylko jednego, podczas gdy drugi jest zwolniony, nie wywołuje żadnej reakcji. Dopiero zwarcie obu przycisków sprawia, że prąd może popłynąć przez cały obwód. Działanie układu w praktyce widoczne jest na poniższych zdjęciach:
- Oba przyciski puszczone – dioda wyłączona.
- Oba przyciski wciśnięte – dioda świeci.
- Pierwszy przycisk wciśnięty – dioda wyłączona.
- Drugi przycisk wciśnięty – dioda wyłączona.
Pomarańczowa linia wskazuje, którą drogą w danej sytuacji popłynie prąd:
- Oba przyciski puszczone – dioda wyłączona.
- Oba przyciski wciśnięte – dioda świeci.
- Pierwszy przycisk wciśnięty – dioda wyłączona.
- Drugi przycisk wciśnięty – dioda wyłączona.
Zanegowana suma - NOR
Niekiedy bardzo przydaje się funktor, który zawiera w sobie dodatkowo negację.
Uwaga: zanegowane jest tylko wyjście!
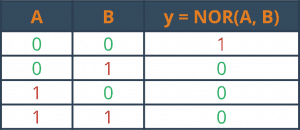
Czyli NOR daje w wyniku 1 tylko, gdy wszystkie argumenty wejściowe są zerami. Działanie tego funktora w formie tabelki wygląda następująco:
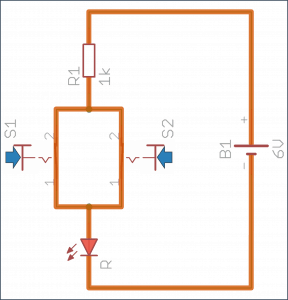
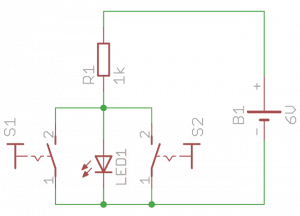
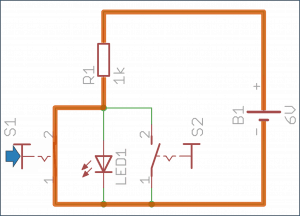
Również tutaj wystarczą te same elementy, aby sprawdzić działanie tej funkcji w praktyce. Teraz trzeba połączyć je zgodnie z poniższym schematem.
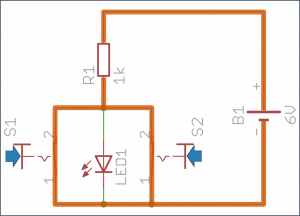
Sytuacja w tym układzie wygląda podobnie jak w negatorze: wciśnięcie któregokolwiek przycisku odprowadza prąd bezpośrednio do masy, z pominięciem diody. Jeżeli wciśnięte są oba przyciski, reakcja układu nie zmienia się - prąd rozkłada się pomiędzy styki i nadal omija diodę.
- Oba przyciski wciśnięte – dioda wyłączona.
- Pierwszy przycisk wciśnięty – dioda wyłączona.
- Drugi przycisk wciśnięty – dioda wyłączona.
- Oba przycisku puszczone – dioda świeci.
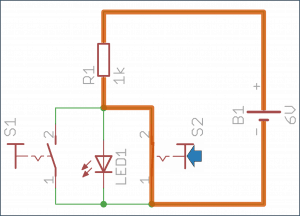
Pomarańczowa linia wskazuje, którą drogą w danej sytuacji popłynie prąd:
- Oba przyciski wciśnięte – dioda wyłączona.
- Pierwszy przycisk wciśnięty – dioda wyłączona.
- Drugi przycisk wciśnięty – dioda wyłączona.
- Oba przyciski puszczone – dioda świeci.
Zanegowany iloczyn - NAND
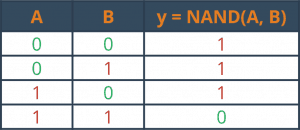
W wyniku zanegowanego iloczynu (NAND) otrzymujemy 0 tylko wtedy, kiedy wszystkie argumenty wejściowe są jedynkami. Działa tak samo, jak bramka AND z dołożoną negacją wyjścia.
W formie tabeli działanie tej funkcji można przedstawić następująco:
NOR i NAND są łatwe do zrealizowania w strukturach krzemowych, dlatego
częściej spotyka się właśnie wersje zanegowane, niż podstawowe (OR i AND).
Bazując na zdobytej już wiedzy oraz poprzednich eksperymentach, postaraj się samodzielnie zbudować układ, który zadziała jak bramka NAND. Oczywiście do jego wykonania użyj tylko diod, rezystorów i przycisków. Koniecznie pochwal się efektem w komentarzu.
Nawiasy
Na razie nie będziemy korzystać z nawiasów, jednak warto wiedzieć o ich istnieniu. Oczywiście już chyba intuicyjnie wiadomo, że porządkują kolejność wykonywania operacji.
1 · (0 + 0) = 1 · 0 = 0
~(1 · 0) + (0 + 1) = ~0 + 1 = 1 + 1 = 1
W ramach ćwiczenia, rozwiąż poniższe równania, korzystając z zasad algebry Boole'a. Swoimi wynikami podziel się w komentarzu!
- ((0 + 1 + 0) · (0 NAND 1)) NOR 1 = ?
- 1 NAND 1 NAND (1 NOR 0) = ?
- (~1 + 1 NOR 0) · (~(0 · 1) + (0 NOR 0)) = ?
Podsumowanie
Podczas tego artykułu poznaliśmy podstawy funkcjonowania cyfrowych układów logicznych. Najważniejsze, aby zapamiętać, czym różnią się operacje wykonywane w algebrze Boole'a od tych tradycyjnych. Od tej pory wszystkie NOTy, ANDy, ORy, NORy i NANDy będą towarzyszyły nam w każdym artykule!
Kluczową umiejętnością po tym artykule będzie samodzielne narysowanie tabel,
które tu się pojawiły i odniesienie ich zawartości do praktyki, czyli zrozumienie, jak wartości z tabeli przekładają się na stany wejść i wyjść układów.
W następnej części zajmiemy się budową bardziej złożonych układów logicznych z zastosowaniem scalonych układów cyfrowych. Poznamy również symbole bramek logicznych i uporządkujemy wiedzę dotyczącą poznanych tutaj funktorów.
Nawigacja kursu
Autorzy: Michał Kurzela, Damian Szymański
Ilustracje: Piotr Adamczyk
To nie koniec, sprawdź również
Przeczytaj powiązane artykuły oraz aktualnie popularne wpisy lub losuj inny artykuł »
algebra, and, bool, funktor, kurs, kursTechnikaCyfrowa, nand, nor, not, or





































Trwa ładowanie komentarzy...